2018-2019学年初中数学北师大版九年级下册第三章《圆》检测题B
试卷更新日期:2019-03-05 类型:单元试卷
一、选择题
-
1. 如图,点A,B,C,D在⊙O上,∠AOC=140°,点B是 的中点,则∠D的度数是( )
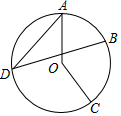 A、70° B、55° C、35.5° D、35°2. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A、70° B、55° C、35.5° D、35°2. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )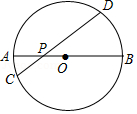 A、 B、2 C、2 D、83. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm4. 如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动点.当点D到弦OB的距离最大时,tan∠BOD的值是( )
A、 B、2 C、2 D、83. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm4. 如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动点.当点D到弦OB的距离最大时,tan∠BOD的值是( )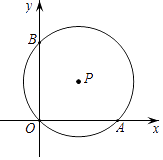 A、2 B、3 C、4 D、55. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A、2 B、3 C、4 D、55. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )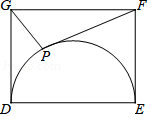 A、 B、
A、 B、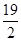 C、34
D、10
6. 如图,若△ABC内接于半径为R的⊙O,且∠A=60°,连接OB、OC,则边BC的长为( )
C、34
D、10
6. 如图,若△ABC内接于半径为R的⊙O,且∠A=60°,连接OB、OC,则边BC的长为( )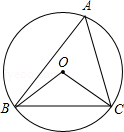 A、
A、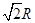 B、
B、 C、
C、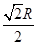 D、 R
7. 以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )A、0≤b<2 B、﹣2
D、 R
7. 以坐标原点O为圆心,作半径为2的圆,若直线y=﹣x+b与⊙O相交,则b的取值范围是( )A、0≤b<2 B、﹣2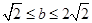 C、﹣2
C、﹣2 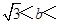 2
D、﹣2 <b<2
8. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
2
D、﹣2 <b<2
8. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( ) A、3 B、3 C、6 D、99. 在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线y= 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为( )A、3 B、2 C、 D、10. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A、3 B、3 C、6 D、99. 在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线y= 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为( )A、3 B、2 C、 D、10. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )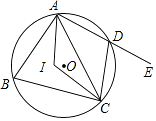 A、56° B、62° C、68° D、78°11. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( )
A、56° B、62° C、68° D、78°11. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( ) A、30° B、36° C、45° D、72°12. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 于点E,以点O为圆心,OC的长为半径作 交OB于点D.若OA=4,则图中阴影部分的面积为( )
A、30° B、36° C、45° D、72°12. 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交 于点E,以点O为圆心,OC的长为半径作 交OB于点D.若OA=4,则图中阴影部分的面积为( )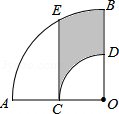 A、 + B、 +2 C、 + D、2 +
A、 + B、 +2 C、 + D、2 +二、填空题
-
13. 已知 的半径为 , , 是 的两条弦, , , ,则弦 和 之间的距离是 .
14. 如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA= .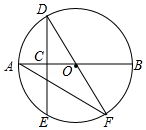 15. 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .
15. 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAB=60°,弦AD平分∠CAB,若AD=6,则AC= .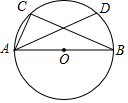 16. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为 .
16. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为 .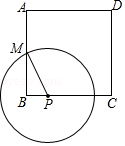 17. 如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
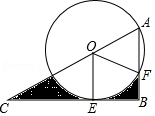
17. 如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .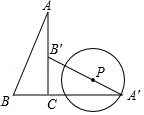 18. 如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以
18. 如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是 .
三、解答题
-
19. 如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
 (1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求 的长.20. 如图,点 在⊙ 的直径 的延长线上,点 在⊙ 上, , .
(1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求 的长.20. 如图,点 在⊙ 的直径 的延长线上,点 在⊙ 上, , . (1)、求证: 是⊙ 的切线;(2)、若⊙ 的半径为 ,求图中阴影部分的面积.
(1)、求证: 是⊙ 的切线;(2)、若⊙ 的半径为 ,求图中阴影部分的面积.
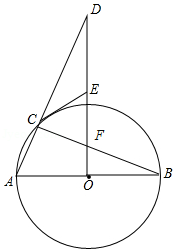
21. 如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.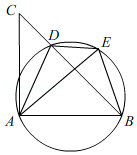 (1)、求证:AE=AB.(2)、若∠CAB=90°,cos∠ADB= ,BE=2,求BC的长.22. 如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
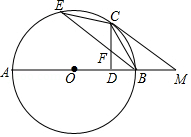
(1)、求证:AE=AB.(2)、若∠CAB=90°,cos∠ADB= ,BE=2,求BC的长.22. 如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.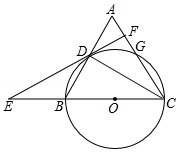 (1)、求证:DF⊥AC;(2)、求tan∠E的值.23. 如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)、求证:DF⊥AC;(2)、求tan∠E的值.23. 如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.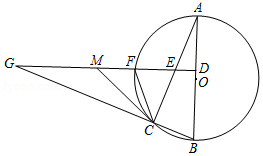 (1)、判断CM与⊙O的位置关系,并说明理由;(2)、若∠ECF=2∠A,CM=6,CF=4,求MF的长.
(1)、判断CM与⊙O的位置关系,并说明理由;(2)、若∠ECF=2∠A,CM=6,CF=4,求MF的长.