2018-2019学年初中数学北师大版九年级下册第三章《圆》检测题 A
试卷更新日期：2019-03-05 类型：单元试卷
一、选择题
-
1. 已知⊙O的半径为5cm，圆心O到直线l的距离为5cm，则直线l与⊙O的位置关系为（ ）
A、相交 B、相切 C、相离 D、无法确定2. 如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（ ）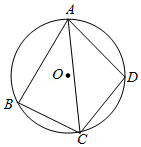
A、AB=AD B、BC=CD C、
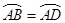D、∠BCA=∠DCA
3. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（ ）
A、8cm B、5cm C、3cm D、2cm4. 《九章算术》是我国古代第一部自成体系的数学专著，代表了东方数学的最高成就．它的算法体系至今仍在推动着计算机的发展和应用．书中记载：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深1寸（ED=1寸），锯道长1尺（AB=1尺=10寸）”，问这块圆柱形木材的直径是多少？”如图所示，请根据所学知识计算：圆柱形木材的直径AC是（ ）
A、13寸 B、20寸 C、26寸 D、28寸5. 如图，边长为1的小正方形构成的网格中，半径为1的⊙O的圆心O在格点上，则∠BED的正切值等于（ ）
A、 B、
C、2
D、
6. 如图所示，四边形ABCD为⊙O的内接四边形，∠BCD=120°，则∠BOD的大小是（ ）
A、80° B、120° C、100° D、90°7. 如图，在△ABC中，∠ACB=90°，过B，C两点的⊙O交AC于点D，交AB于点E，连接EO并延长交⊙O于点F.连接BF，CF.若∠EDC=135°，CF= ，则AE2+BE2的值为（ ）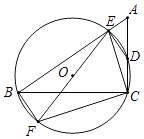
A、8 B、12 C、16 D、208. 如图，△ABC内接于⊙O，若sin∠BAC= ，BC=2 ，则⊙O的半径为（ ）
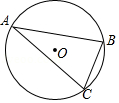A、3 B、6 C、4 D、29. 如图，直线AB与⊙O相切于点A，AC、CD是⊙O的两条弦，且CD∥AB，若⊙O的半径为5，CD=8，则弦AC的长为（ ）
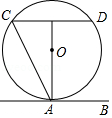A、10 B、8 C、4 D、410. 如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC=124°，点E在AD的延长线上，则∠CDE的度数为（ ）
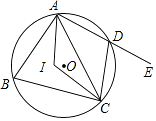A、56° B、62° C、68° D、78°11. 已知圆内接正三角形的面积为 ，则该圆的内接正六边形的边心距是（ ）A、2 B、1 C、 D、12. 如图，从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为（ ）
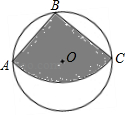A、
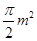B、
C、πm2
D、2πm2
二、填空题
-
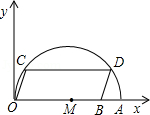
13. 如图，在平面直角坐标系中，点A的坐标是（20，0），点B的坐标是（16，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，则点C的坐标为 ．
14. 如图，半圆的半径OC=2，线段BC与CD是半圆的两条弦，BC=CD，延长CD交直径BA的延长线于点E，若AE=2，则弦BD的长为 ．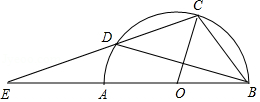
15. 如图，AD为△ABC的外接圆⊙O的直径，若∠BAD=50°，则∠ACB=°．
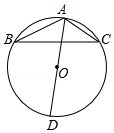16. 如图，AC为⊙O的直径，点B在圆上，OD⊥AC交⊙O于点D，连接BD，∠BDO=15°，则∠ACB= ．
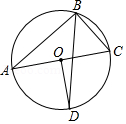17. 已知直线y=kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为 ．18. 如图，△OAC的顶点O在坐标原点，OA边在x轴上，OA=2，AC=1，把△OAC绕点A按顺时针方向旋转到△O′AC′，使得点O′的坐标是（1， ），则在旋转过程中线段OC扫过部分（阴影部分）的面积为 ．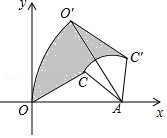
三、解答题
-
19. 如图，在△ABC中，AB=AC，以AB为直径的圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．
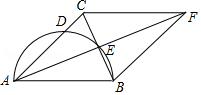(1)、求证：四边形ABFC是菱形；(2)、若AD=7，BE=2，求半圆和菱形ABFC的面积．20. 如图AB是⊙O的直径，PA与⊙O相切于点A，BP与⊙O相交于点D，C为⊙O上的一点，分别连接CB、CD，∠BCD=60°．
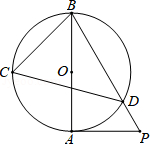(1)、求∠ABD的度数；(2)、若AB=6，求PD的长度．21. 如图，在△ABC中，以BC为直径的⊙O交AC于点E，过点E作AB的垂线交AB于点F，交CB的延长线于点G，且∠ABG=2∠C．
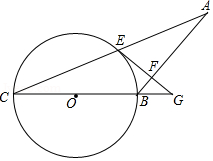(1)、求证：EG是⊙O的切线；(2)、若tanC= ，AC=8，求⊙O的半径．22. 如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．
(1)、求证：AE=ED；(2)、若AB=10，∠CBD=36°，求 的长．23. 如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB，连接DO并延长交CB的延长线于点E．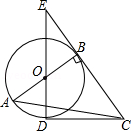
(1)、判断直线CD与⊙O的位置关系，并说明理由；(2)、若BE=4，DE=8，求AC的长．24. 已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF的延长线于点D，垂足为点D．
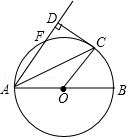(1)、求扇形OBC的面积（结果保留π）；(2)、求证：CD是⊙O的切线．25. 如图，D是△ABC外接圆上的动点，且B，D位于AC的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．
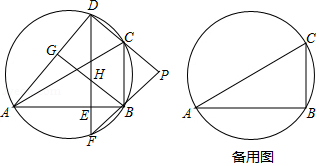(1)、求证：BG∥CD；(2)、设△ABC外接圆的圆心为O，若AB= DH，∠OHD=80°，求∠BDE的大小．