2018-2019学年初中数学华师大版八年级下册第十九章 矩形、菱形与正方形 单元检测B卷
试卷更新日期：2019-03-05 类型：单元试卷
一、选择题
-
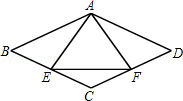
1. 如图，已知四边形ABCD的四边都相等，等边△AEF的顶点E，F分别在BC，CD上，且AE=AB，则∠C=（ ）
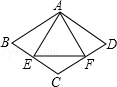A、100° B、105° C、110° D、120°2. 如图，已知E是菱形ABCD的边BC上一点，且∠DAE=∠B=80°，那么∠CDE的度数为（ ）
A、20° B、25° C、30° D、35°3. 如图，把菱形ABCD沿AH折叠，使B点落在BC上的E点处，若∠B=70°，则∠EDC的大小为（ ）
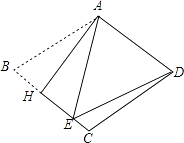A、10° B、15° C、20° D、30°4. 如果平行四边形的四个内角的平分线能够围成一个四边形，那么这个四边形一定是（ ）A、平行四边形 B、矩形 C、菱形 D、正方形5. 如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（ ）
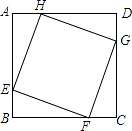A、30 B、34 C、36 D、406. 如图，一张矩形纸片沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形），则∠OCD等于（ ）
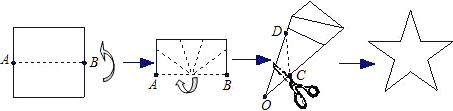A、108° B、114° C、126° D、129°7.如图，在矩形ABCD中，AB=6，BC=8，AC与BD相交于O，E为DC的一点，过点O作OF⊥OE交BC于F．记d= ， 则关于d的正确的结论是（ ）
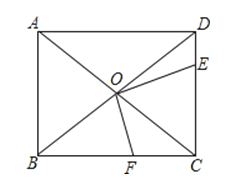A、d=5 B、d＜5 C、d≤5 D、d≥58. 如图，点A，B在直线l上两点，以AB为边作菱形ABCD，M、N分别是BC和CD的中点，NP⊥AB于点P，连接MP，若∠D=140°，则∠MPB的度数为（ ）
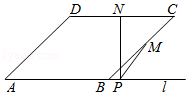A、100° B、110° C、120° D、130°9. 如图，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC=EC，连结DF交BE的延长线于点H，连结OH交DC于点G，连结HC．则以下四个结论中：①OH∥BF，②GH= BC，③OD= BF，④∠CHF=45°．正确结论的个数为（ ）
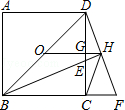A、4个 B、3个 C、2个 D、1个10. 如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E，F同时由A，C两点出发，分别沿AB，CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为（ ）
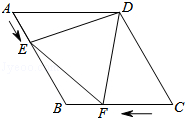A、1 B、
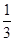C、
D、
二、填空题（共6小题）
-
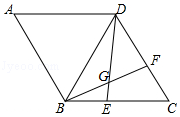
11. 如图，在菱形ABCD中，AB=BD，点E，F分别在BC，CD边上，且CE=DF，BF与DE交于点G，若BG=2，DG=4，则CD长为 ．
12. 如图，已知菱形ABCD的对角线AC、BD相交于点O，AB=6cm，E是CD的中点，则OE的长为cm．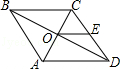
13. 矩形ABCD的对角线AC，BD相交于点O，请你添加一个适当的条件 ， 使其成为正方形（只填一个即可）14. 如果用4个相同的长为3宽为1的长方形，拼成一个大的长方形，那么这个大的长方形的周长可以是 ．15. 如图，在菱形ABCD中，AC=6cm，BD=8cm，则菱形ABCD的高AE为cm．
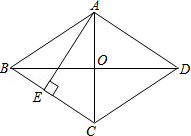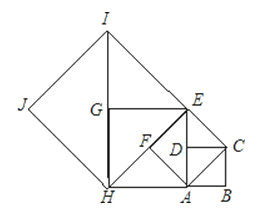
16.如图所示，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以AE为边作第三个正方形AEGM，…已知正方形ABCD的面积S1=1，按上述方法所作的正方形的面积依次为S2 ， S3 ， …Sn（n为正整数），那么第8个正方形面积S8=
三、解答题
-
17. 已知：如图，在△ABC中，AB=AC，点D为BC中点，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．求证：四边形ADCE为矩形．
18. 如图，在▱ABCD中，AC、BD相交于点O，△AOB是等边三角形，AB=4cm，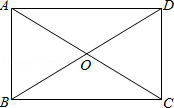
(1)、判断▱ABCD是矩形吗？说说你的理由．(2)、求▱ABCD的面积．19. 如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
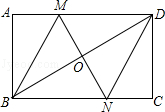(1)、求证：四边形BMDN是菱形；(2)、若AB=4，AD=8，求菱形BMDN的面积和对角线MN的长．20. 已知，如图，在三角形ABC中，CD是中线，过点A作平行线BC的平行线，交CD的延长线于点E，连接EB．
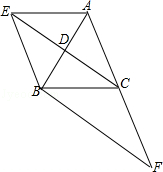(1)、求证：四边形AEBC是平行四边形；(2)、延长AC到点F，使CF=AC，连接BF，当三角形ABF满足条件时，四边形AEBC是菱形？请证明．21. 如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于点D，交AB于点E，点F在DE的延长线上，且AF=CE．
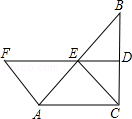(1)、四边形ACEF是平行四边形吗？说明理由；(2)、当∠B的大小满足什么条件时，四边形ACEF为菱形？请说明你的结论；(3)、四边形ACEF有可能是正方形吗？为什么？
