2018-2019学年初中数学华师大版八年级下册19.3 正方形 同步练习
试卷更新日期：2019-03-05 类型：同步测试
一、选择题
-
1. 要使菱形ABCD成为正方形，需要添加的条件是（ ）A、AB=CD B、AD=BC C、AB=BC D、AC=BD2. 正方形具有而矩形不一定具有的性质是（ ）A、四个角都是直角 B、对角线互相垂直 C、对角线相等 D、两对角线将其分割的四个三角形面积相等3. 如图，在正方形ABCD中，点E，F分别在边BC，CD上，且BE=CF．连接AE，BF，AE与BF交于点G．下列结论错误的是（ ）
A、AE=BF B、∠DAE=∠BFC C、∠AEB+∠BFC=90° D、AE⊥BF4. 如图，▱ABCD中，E为BC边上一点，以AE为边作正方形AEFG，若∠BAE=40°，∠CEF=15°，则∠D的度数是（ ）
A、65° B、55° C、70° D、75°5. 如图，正方形ABCD的对角线AC，BD相交于点O，DE平分∠ODA交OA于点E，若AB=4，则线段OE的长为（ ）
A、
B、4﹣2
C、
D、 ﹣2
6. 如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5，则四边形EFGH的面积是（ ）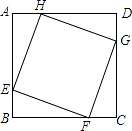
A、30 B、34 C、36 D、407.如图，四边形ABCD中，AD=DC，∠ADC=∠ABC=90°，DE⊥AB，若四边形ABCD面积为16，则DE的长为（ ）
A、3 B、2 C、4 D、88. 如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列结论：①OA=OD；
②AD⊥EF；
③AE+DF=AF+DE；
④当∠BAC=90°时，四边形AEDF是正方形．
其中一定正确的是（ ）
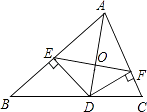A、①②③ B、②③④ C、①③④ D、①②③④9. 如图．边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是（ ）
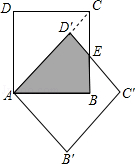A、
B、
C、
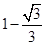D、
二、填空题
-
10. 如图，AC是正方形ABCD的对角线，∠DCA的平分线交BA的延长线于点E，若AB=3，则AE=
11. 如图，点P是正方形ABCD的对角线BD上的一个动点（不与B、D重合），连结AP，过点B作直线AP的垂线，垂足为H，连结DH．若正方形的边长为4，则线段DH长度的最小值是 ．
12. 已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，其中错误的是 （只填写序号）．13. 如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是边BM、CM的中点，当AB：AD=时，四边形MENF是正方形．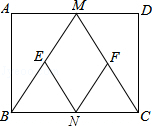
14. 如图，在四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DP⊥AB于P．若四边形ABCD的面积是18，则DP的长是 ．
三、解答题
-
15. 如图，正方形ABCD中，E、F分别是AB和AD上的点，已知CE⊥BF，垂足为M，请找出和BE相等的线段，并证明你的结论．
16. 如图，已知在正方形ABCD中，AE∥BD，BE=BD，BE交AD于F．求证：DE=DF．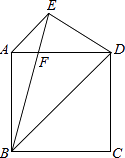
17. 如图，已知正方形ABCD，E是AB延长线上一点，F是DC延长线上一点，连接BF，EF，恰有BF=EF，将线段EF绕点F顺时针旋转90°得FG，过点B作EF的垂线，交EF于点M，交DA的延长线于点N，连接NG．
(1)、求证：BE=2CF；(2)、试猜想四边形BFGN是什么特殊的四边形，并对你的猜想加以证明．
