2018-2019学年初中数学华师大版八年级下册19.2.2 菱形的判定 同步练习
试卷更新日期：2019-03-05 类型：同步测试
一、选择题
-
1. 如图，在△ABC中，点D，E，F分别在边AB，BC，CA上，且DE∥CA，DF∥BA．
下列四种说法：
①四边形AEDF是平行四边形；②如果∠BAC=90°，那么四边形AEDF是矩形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果AD⊥BC且AB=AC，那么四边形AEDF是菱形．其中，正确的有（ ） 个．
A、1 B、2 C、3 D、42. 如图，在平行四边形ABCD中，对角线AC、BD交于点O，添加下列一个条件，能使平行四边形ABCD成为菱形的是（ ）
A、AO=BO B、AC=AD C、AB=BC D、OD=AC3. 如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，DE=DF．在下列条件中，使四边形BECF是菱形的是（ ）
A、EB⊥EC B、AB⊥AC C、AB=AC D、BF∥CE4. 如图，剪两张对边平行的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）
A、∠ABC=∠ADC，∠BAD=∠BCD B、AB=BC C、AB=CD，AD=BC D、∠DAB+∠BCD=180°5. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．若BF=12，AB=10，则AE的长为（ ）
A、10 B、12 C、16 D、186. 如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，以A为圆心，AB长为半径画弧交AD于F，若BF=12，AB=10，则AE的长为（ ）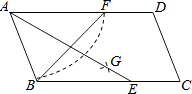
A、16 B、15 C、14 D、137. 如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是（ ）
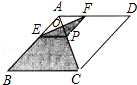A、2 B、 C、3 D、二、填空题
-
8.
如图四边形ABCD的对角线互相垂直，且OB=OD，请你添加一个适当的条件使它成为菱形（只需添加一个）
9. 如图，在▱ABCD中，AB=5，AC=6，当BD=时，四边形ABCD是菱形．
10.已知，如图，△ABC中，E为AB的中点，DC∥AB，且DC=AB，请对△ABC添加一个条件： ， 使得四边形BCDE成为菱形．
11. 如图，在∠MON的两边上分别截取OA、OB，使OA=OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB=2cm，四边形OACB的面积为4cm2 ． 则OC的长为cm．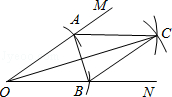
12. 如图，矩形ABCD的对角线AC、BD相交于点O，∠AOB=120°，CE∥BD，DE∥AC，若AD=4，则四边形CODE的周长 ．
13. 如图，AD是△ABC的角平分线，DE∥AC交AB于E，DF∥AB交AC于F．且AD交EF于O，则∠AOF=度．
14. （如图所示）两个长宽分别为7cm、3cm的矩形如图叠放在一起，则图中阴影部分的面积是 ．
15.如图，在菱形ABCD中，过对角线BD上任一点P，作EF∥BC，GH∥AB，下列结论正确的是 ．（填序号）
①图中共有3个菱形；
②△BEP≌△BGP；
③四边形AEPH的面积等于△ABD的面积的一半；
④四边形AEPH的周长等于四边形GPFC的周长．
三、解答题
-
16. 如图，在Rt△ABC中，∠ACB=90°，CD是AB边上的中线，过点B作BE∥CD，过点C作CE∥AB，BE，CE相交于点E．
求证：四边形BDCE是菱形．
17. 如图，△ABC中，AB=AC，∠BAC=40°，将△ABC绕点A按逆时针方向旋转100°．得到△ADE，连接BD，CE交于点F．
(1)、求证：△ABD≌△ACE；(2)、求证：四边形ABFE是菱形．18. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，BD=8．
(1)、求证：四边形ABCD是菱形；(2)、过点A作AH⊥BC于点H，求AH的长．19. 如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，且AD=4，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．
(1)、求CE的长；(2)、当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由．
