2018-2019学年初中数学华师大版八年级下册第十八章平行四边形 单元检测提高卷
试卷更新日期：2019-03-05 类型：单元试卷
一、选择题
-
1. 如图，四边形ABCD是平行四边形，BE平分∠ABC，CF平分∠BCD，BE、CF交于点G．若使EF= AD，那么平行四边形ABCD应满足的条件是（ ）
A、∠ABC=60° B、AB：BC=1：4 C、AB：BC=5：2 D、AB：BC=5：82. 在面积为12的平行四边形ABCD中，过点A作直线BC的垂线交直线BC于点E，过点A作直线CD的垂线交直线CD于点F，若AB=4，BC=6，则CE+CF的值为（ ）A、
B、
C、 或 
D、 或
3. 如图，在 ▱ ABCD中，AB=4，AD=7，∠ABC平分线交AD于点E，交CD的延长线于点F，则DF的长是（ ）
A、2 B、3 C、4 D、54. 如图，已知口ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=45°，则∠DA′E′的大小为（ ）
A、170° B、165° C、160° D、155°5.如图，平行四边形ABCD中，E是AB上一点，DE、CE分别是∠ADC、∠BCD的平分线，若AD=5，DE=6，则平行四边形的面积为（ ）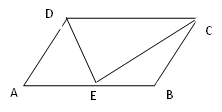
A、96 B、48 C、60 D、306. 如图，▱ABCD的周长为32cm，AC，BD相交于点O，OE⊥AC交AD于点E，则△DCE的周长为 （ ）
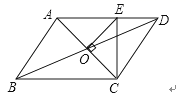A、24cm B、16cm C、8cm D、10cm7.已知▱ABCD中，AD=2AB，F是BC的中点，作AE⊥CD，垂足E在线段CD上，连结EF、AF，下列结论：①2∠BAF=∠BAD；②EF=AF；③S△ABF≤S△AEF；④∠BFE=3∠CEF．中一定成立的是（ ）
A、①②④ B、①③ C、②③④ D、①②③④8. 四边形ABCD中，对角线AC与BD交于点O，下列条件中不一定能判定这个四边形是平行四边形的是（ ）A、AB＝DC，∠ABC＝∠ADC B、AD∥BC，AB∥DC C、AB＝DC，AD＝BC D、OA＝OC，OB＝OD9. 四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD，从中任选两个条件，能使四边形ABCD为平行四边形的选法有（ ）．A、3种 B、4种 C、5种 D、6种10. 在▱ABCD中，对角线AC，BD相交于O点，AC＝10，BD＝8，则AD长的取值范围是（ ）A、AD＞1 B、AD＜9 C、1＜AD＜9 D、AD＞1011. 如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，联结EF、CF，那么下列结论中一定成立的个数是（ ）①∠DCF= ∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．
A、1个 B、2个 C、3个 D、4个12. 将一张平行四边形纸片折一次，使得折痕平分这个平行四边形的面积，则这样的折纸方法有（ ）A、1种 B、2种 C、3种 D、无数种二、填空题
-
13. 在四边形ABCD中，AD∥BC，分别添加下列条件之一：①AB∥CD；②AB＝CD；③∠A＝∠C；④∠B＝∠C.能使四边形ABCD为平行四边形的条件的序号是 ．14. 在平行四边形 中， 平分 交边 于 ， 平分 交边 于 .若 ， ，则 .15. 如图，已知▱OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为 ．
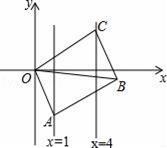16. 如图，AB∥CD， AD∥BC，点E、F分别是线段BC和CD上的动点，在两点运动到某一位置时，恰好使得∠AEF=∠AFE ， 此时量得∠BAE=15°，∠FEC=12°，∠DAF=25°，则∠EFC=°
17. 如图，以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE，使AD=DE=CE，∠DEC=90°，且点E在平行四边形内部，连接AE、BE，则∠AEB的度数是.
18. 如图，在△ABC中，AB=5，AC=12，BC=13，△ABD、△ACE、△BCF都是等边三角形，则四边形AEFD的面积S= ．
三、解答题
-
19. 已知▱ABCD的周长为36cm，过点A作AE⊥BC，AF⊥CD，垂足分别为E、F.若AE＝2cm，AF＝4cm.求▱ABCD的各边长．
20. 如图，在四边形ABCD中，AD=BC，BE=DF，AE⊥BD，CF⊥BD，垂足分别为E，F，求证：四边形AFCE是平行四边形．
21. 如图，在四边形ABCD中，AD∥BC，AD=6，BC=16，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．当运动时间t为多少秒时，以点P，Q，E，D为顶点的四边形是平行四边形．
22. 如图所示，已知平行四边形ABCD的对角线交于O，过O作直线交AB、CD的反向延长线于E、F，求证：OE＝OF.
23. 如图，四边形ABCD是矩形，点E在CD边上，点F在DC延长线上，AE=BF．
(1)、求证：四边形ABFE是平行四边形；(2)、若∠BEF=∠DAE，AE=3，BE=4，求EF的长．24. 如图，在平行四边形ABCD中，∠ABC＝120°，∠BAD的平分线交BC于点E，交DC的延长线于点F，过点F作FG∥CE，且FG＝CE，连结DG，EG，BG，CG.
(1)、试判断四边形EGFC的形状；(2)、求证：△DCG≌△BEG；(3)、试求出∠BDG的度数．
