2018-2019学年初中数学华师大版八年级下册18.2 平行四边形的判定（1）同步练习
试卷更新日期：2019-03-05 类型：同步测试
一、选择题
-
1. 如图，AB＝CD＝EF，且△ACE≌△BDF，则图中平行四边形的个数为（ ）
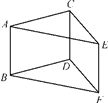A、1 B、2 C、3 D、42. 如图，将平行四边形ABCD沿
翻折，使点 
恰好落在 
上的点 
处，则下列结论不一定成立的是（ ） 
A、AF=EF B、AB=EF C、AE=AF D、AF=BE3. 如图，平行四边形ABCD中，∠ABC=45°，E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，AB=1，则EF的长是（ ）
A、1.5 B、
C、
D、2
4. 已知四边形ABCD的四条边分别是a、b、c、d．其中a、c是对边，且a2+b2+c2+d2=2ac+2bd，则四边形一定是（ ）A、平行四边形 B、矩形 C、菱形 D、正方形5. 如图是某城市部分街道，已知AF∥BC，EC⊥BC，EF＝CF，BA∥DE，BD∥AE，甲、乙两人同时从B站乘车到F站，甲乘1路车，路线是B→A→E→F；乙乘2路车，路线是B→D→C→F.假设两车速度相同，途中耽误的时间相同，那么（ ）
A、甲将先到F站 B、乙将先到F站 C、甲、乙将同时到达 D、不能确定6. 如图，在Rt△ABC中，∠C=90°，点D是AC边上的动点，过点D作DE∥AB交CB于E，过点B作BF⊥BC交DE的延长线于F，当AD从小于DC到大于DC的变化过程中，则△DCE与△BEF的周长之和的变化情况是（ ）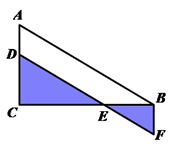
A、一直不变 B、一直增大 C、先增大后减小 D、先减小后增大7. 如图所示，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是（ ）
A、5 B、10 C、15 D、20二、填空题
-
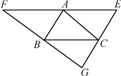
8. 若四边形ABCD的边AB＝CD，BC＝DA，则这个四边形是 ， 理由是 ．9. 如图，AB∥EG，EF∥BC，AC∥FG，图中有个平行四边形，它们分别是 ．
10. 如图，在Rt△ABC中，∠BAC＝90°，AB＝4，AC＝3，点D，E分别是AB，AC的中点，点G，F在BC边上(均不与端点重合)，DG∥EF.将△BDG绕点D顺时针旋转180°，将△CEF绕点E逆时针旋转180°，拼成四边形MGFN，则四边形MGFN周长l的取值范围是.
11. 如图，四边形ABCD是平行四边形，∠ABC=70°，BE平分∠ABC且交AD于点E，DF∥BE且交BC于点F，则∠1的度数为 ．
三、解答题
-
12. 如图所示，在△ABC中，∠ACB＝90°点E是AB的中点，连接CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF＝CE，求证四边形ACEF是平行四边形．
13. 如图所示，在
ABCD中，E，F，G，H分别是四条边上的点，且满足AE＝CF，BG＝DH，连接EF，GH．试说明EF和GH互相平分． 
14. 如图，已知E，F，G，H分别是平行四边形ABCD的边AB，BC，CD，DA上的点，且AE=CG，BF=DH．求证：四边形EFGH是平行四边形．
15. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图1，在四边形ABCD中，BC=AD，AB=
求证：四边形ABCD是 四边形．
(1)、在方框中填空，以补全已知和求证；(2)、按嘉淇同学的思路写出证明过程；(3)、用文字叙述所证命题的逆命题.
