浙江省浙南名校联盟2018-2019学年高三上学期数学期末联考试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 设集合 , ,则 ( )A、
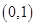 B、
B、 C、
C、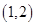 D、
D、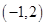 2. 双曲线 的焦点坐标为( )A、
2. 双曲线 的焦点坐标为( )A、 B、
B、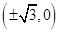 C、
C、 D、
D、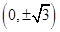 3. 设实数 满足 ,则 的最小值为( )A、
3. 设实数 满足 ,则 的最小值为( )A、 B、
B、 C、
C、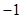 D、
D、 4. 若复数 , ,其中 是虚数单位,则 的最大值为( )A、
4. 若复数 , ,其中 是虚数单位,则 的最大值为( )A、 B、
B、 C、
C、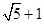 D、
D、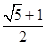 5. 函数 的图象可能是( )A、
5. 函数 的图象可能是( )A、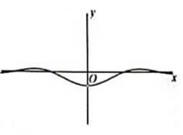 B、
B、 C、
C、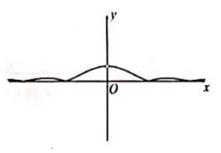 D、
D、 6. 已知 , ,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 甲、乙二人均从5种不同的食品中任选一种或两种吃,则他们一共吃到了3种不同食品的情况有( )A、84种 B、100种 C、120种 D、150种8. 已知随机变量 的分布列如下表:
6. 已知 , ,则 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 甲、乙二人均从5种不同的食品中任选一种或两种吃,则他们一共吃到了3种不同食品的情况有( )A、84种 B、100种 C、120种 D、150种8. 已知随机变量 的分布列如下表:X
-1
0
1
P
a
b
c
其中 .若 的方差 对所有 都成立,则( )
A、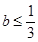 B、
B、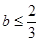 C、
C、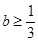 D、
D、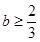 9. 如图,在三棱柱 中,点 在平面 内运动,使得二面角 的平面角与二面角 的平面角互余,则点 的轨迹是( )
9. 如图,在三棱柱 中,点 在平面 内运动,使得二面角 的平面角与二面角 的平面角互余,则点 的轨迹是( ) A、一段圆弧 B、椭圆的一部分 C、抛物线 D、双曲线的一支10. 设 是方程 的两个不等实根,记 .下列两个命题:①数列 的任意一项都是正整数;②数列 第5项为10. ( )A、①正确,②错误 B、①错误,②正确 C、①②都正确 D、①②都错误
A、一段圆弧 B、椭圆的一部分 C、抛物线 D、双曲线的一支10. 设 是方程 的两个不等实根,记 .下列两个命题:①数列 的任意一项都是正整数;②数列 第5项为10. ( )A、①正确,②错误 B、①错误,②正确 C、①②都正确 D、①②都错误二、填空题
-
11. 《九章算术》中记载了“今有共买豕,人出一百,盈一百;人出九十,适足。问人数、豕价各几何?”.其意思是“若干个人合买一头猪,若每人出100,则会剩下100;若每人出90,则不多也不少。问人数、猪价各多少?”.设 分别为人数、猪价,则 , .12. 某三棱锥的三视图如图所示,则该三棱锥的体积为 , 表面积为.
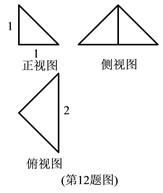 13. 在 中,内角 所对的边分别是 .若 , ,则 , 面积的最大值为.14. 实数 满足:对任意 ,都有 则 = , .15. 已知抛物线 的焦点为 .若抛物线上存在点 ,使得线段 的中点的横坐标为 ,则 .16. 若向量 满足 , 且 ,则 的最小值是.
13. 在 中,内角 所对的边分别是 .若 , ,则 , 面积的最大值为.14. 实数 满足:对任意 ,都有 则 = , .15. 已知抛物线 的焦点为 .若抛物线上存在点 ,使得线段 的中点的横坐标为 ,则 .16. 若向量 满足 , 且 ,则 的最小值是.
17. 已知函数 在开区间 上单调递减,则 的取值范围是.三、解答题
-
18. (I)证明: ;
(II)求函数 的最小正周期与单调递增区间.
19. 在三棱台 中, 是等边三角形,二面角 的平面角为 , .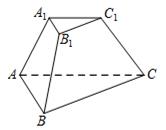
(I)求证: ;
(II)求直线 与平面 所成角的正弦值.