浙江省衢州五校2018-2019学年高一上学期数学期末联考试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 =( )A、
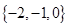 B、
B、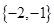 C、
C、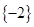 D、
D、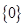 2. 的值是( )A、
2. 的值是( )A、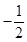 B、
C、
B、
C、 D、
D、 3. 下列函数中,既是偶函数又在区间 上单调递增的函数是( )A、
3. 下列函数中,既是偶函数又在区间 上单调递增的函数是( )A、 B、
B、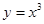 C、
C、 D、
D、 4. 设 ,则( )A、
4. 设 ,则( )A、 B、
B、 C、
C、 D、
D、 5. 函数 的图象为( )A、
5. 函数 的图象为( )A、 B、
B、 C、
C、 D、
D、 6. 已知函数 ,若函数 有两个不同的零点,则 的取值范围( )A、 B、
6. 已知函数 ,若函数 有两个不同的零点,则 的取值范围( )A、 B、 C、
C、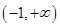 D、
D、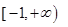 7. 对于函数 ,给出下列选项其中正确的是( )A、函数
7. 对于函数 ,给出下列选项其中正确的是( )A、函数 的图象关于点
的图象关于点  对称
B、存在
对称
B、存在  ,使
,使  C、存在
C、存在  ,使函数
,使函数  的图象关于 y 轴对称
D、存在
的图象关于 y 轴对称
D、存在  ,使
,使  恒成立
8. 如图,点 在圆 上,且点 位于第一象限,圆 与 正半轴的交点是 ,点 的坐标为 , ,若 则 的值为( )
恒成立
8. 如图,点 在圆 上,且点 位于第一象限,圆 与 正半轴的交点是 ,点 的坐标为 , ,若 则 的值为( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 已知 , ,若对任意 , 或 ,则 的取值范围是( )A、
9. 已知 , ,若对任意 , 或 ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 10. 定义在 上的偶函数 满足:当 时有 ,且当 时, ,则函数 的零点个数是( )A、6个 B、7个 C、8个 D、无数个
10. 定义在 上的偶函数 满足:当 时有 ,且当 时, ,则函数 的零点个数是( )A、6个 B、7个 C、8个 D、无数个二、填空题
-
11. 设集合 , ,则 , .12. 已知 ,且 ,则 , .13. 若函数 的周期 ,则 , 且函数 的单调递减区间为.( 是自然对数的底数)14. 函数 的图象恒过定点 , 若函数 的图象的对称轴为 ,则非零实数 的值为.15. 已知 ,若函数 在 是增函数,则 的取值范围是.16. 已知函数 ,当 变化时, 恒成立,则实数 的取值范围是.17. 已知 , ,若 , ,则 .
三、解答题
-
18.(1)、(2)、19. 已知函数 的部分图象如图所示.
 (1)、求函数 的解析式;(2)、将函数 的图象向右平移 个单位得到函数 ,当 时,求函数 的值域.
(1)、求函数 的解析式;(2)、将函数 的图象向右平移 个单位得到函数 ,当 时,求函数 的值域.