浙江省诸暨市2018-2019学年高二上学期数学期末考试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 抛物线 的准线方程是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 , , , , ,则下列不等式成立的是( )A、 B、
2. 已知 , , , , ,则下列不等式成立的是( )A、 B、 C、
C、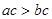 D、
D、 3. 不等式 的解集是( )A、
3. 不等式 的解集是( )A、 B、
B、 C、
C、 D、
D、 4. 直线 , 在平面 内射影也是两条直线,分别是 , ,下列说法正确的是( )A、若
4. 直线 , 在平面 内射影也是两条直线,分别是 , ,下列说法正确的是( )A、若 ,则
,则  B、若
B、若  ,则
,则  C、若
C、若  ,则
,则  D、若
D、若  ,则
,则  5. 已知函数 ,函数的最小值等于( )A、
5. 已知函数 ,函数的最小值等于( )A、 B、
B、 C、5
D、9
6. 某几何体的正视图如图所示,这个几何体不可能是( )
C、5
D、9
6. 某几何体的正视图如图所示,这个几何体不可能是( ) A、圆锥与圆柱的组合 B、棱锥与棱柱的组合 C、棱柱与棱柱的组合 D、棱锥与棱锥的组合7. 如图,正三棱柱 中, , 是 的中点,则 与平面 所成角的正弦值等于( )
A、圆锥与圆柱的组合 B、棱锥与棱柱的组合 C、棱柱与棱柱的组合 D、棱锥与棱锥的组合7. 如图,正三棱柱 中, , 是 的中点,则 与平面 所成角的正弦值等于( ) A、
A、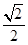 B、
C、
B、
C、 D、
D、 8. 如图,双曲线 的左、右焦点分别是 , , 是双曲线右支上一点, 与圆 相切于点 , 是 的中点,则 ( )
8. 如图,双曲线 的左、右焦点分别是 , , 是双曲线右支上一点, 与圆 相切于点 , 是 的中点,则 ( )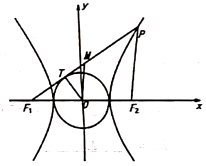 A、1 B、2 C、 D、
A、1 B、2 C、 D、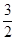 9. 过双曲线 的右焦点 作斜率为 的直线,交两条渐近线于 , 两点,若 ,则此双曲线的离心率等于( )A、
9. 过双曲线 的右焦点 作斜率为 的直线,交两条渐近线于 , 两点,若 ,则此双曲线的离心率等于( )A、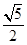 B、
B、 C、
C、 D、
10. 正四面体 的棱 与平面 所成角为 ,其中 ,点 在平面 内,则当四面体 转动时( )A、存在某个位置使得
D、
10. 正四面体 的棱 与平面 所成角为 ,其中 ,点 在平面 内,则当四面体 转动时( )A、存在某个位置使得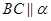 ,也存在某个位置使得
,也存在某个位置使得  B、存在某个位置使得
B、存在某个位置使得 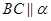 ,但不存在某个位置使得
,但不存在某个位置使得  C、不存在某个位置使得
C、不存在某个位置使得 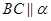 ,但存在某个位置使得
,但存在某个位置使得  D、既不存在某个位置使得
D、既不存在某个位置使得 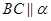 ,也不存在某个位置使得
,也不存在某个位置使得 
二、填空题
-
11. 已知 , 则 , .12. 南北朝数学家何承天发明的“调日法”是程序化寻求精确分数表示近似值的方法,理论依据是:若 ,则 .例如 , ,使用一次“调日法”得到分数 ,范围就缩小到 .若我们要求近似值与 的误差小于0.1,则至少还要使用“调日法”次,相应得到的 的近似分数是.13. 若抛物线的焦点在直线 上,则抛物线的标准方程是.14. 某几何体的三视图如图所示,则该几何体体积为 , 表面积为.
 15. 正方体 的棱长为4,点 是棱 上一点,若异面直线 与 所成角的余弦值为 ,则 .
15. 正方体 的棱长为4,点 是棱 上一点,若异面直线 与 所成角的余弦值为 ,则 . 16. 已知 .若 ,则当 取最大值时, ;若 ,则 的最小值 .17. 已知椭圆 的离心率大于 , 是椭圆的上顶点, 是椭圆上的点,则 的最大值 .
16. 已知 .若 ,则当 取最大值时, ;若 ,则 的最小值 .17. 已知椭圆 的离心率大于 , 是椭圆的上顶点, 是椭圆上的点,则 的最大值 .三、解答题
-
18. 电视台应某企业之约播放两套连续剧,其中,连续剧甲每次播放时间80分钟,其中广告时间1分钟,收视观众60万;连续剧乙每次播放时间40分钟,其中广告时间1分钟,收视观众20万.现在企业要求每周至少播放广告6分钟,而电视台每周至多提供320分钟节目时间.(1)、设每周安排连续剧甲 次,连续剧乙 次,列出 , 所应该满足的条件;(2)、应该每周安排两套电视剧各多少次,收视观众最多?19. 如图,三棱锥 中, , 分别是 , 的中点.
 (1)、求证 平面 ;(2)、若 ,平面 平面 , ,求证: .20. 已知椭圆 上的点 (不包括横轴上点)满足:与 , 两点连线的斜率之积等于 , , 两点也在曲线 上.(1)、求椭圆 的方程;(2)、过椭圆 的右焦点作斜率为1的直线交椭圆于 , 两点,求 ;(3)、求椭圆上的点到直线 距离的最小值.
(1)、求证 平面 ;(2)、若 ,平面 平面 , ,求证: .20. 已知椭圆 上的点 (不包括横轴上点)满足:与 , 两点连线的斜率之积等于 , , 两点也在曲线 上.(1)、求椭圆 的方程;(2)、过椭圆 的右焦点作斜率为1的直线交椭圆于 , 两点,求 ;(3)、求椭圆上的点到直线 距离的最小值.
