浙江省宁波市九校2018-2019学年高二上学期数学期末联考试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 椭圆 的短轴长为( )A、8 B、10 C、5 D、42. 设复数 满足 ,其中 为虚数单位,则复数 对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知 , 是两条不同的直线, , 是两个不同的平面,下列说法正确的是( )A、若
 ,
,  ,
,  ,则
,则  B、若
B、若  ,
,  ,则
,则  C、若
C、若  ,
,  ,则
,则  D、若平面 内有不共线的三点到平面 β 的距离相等,则
D、若平面 内有不共线的三点到平面 β 的距离相等,则  4. 有下列四个命题:
4. 有下列四个命题:①“相似三角形周长相等”的否命题;②“若 ,则 ”的逆命题;③“若 ,则 ”的否命题;④“若 ,则方程 有实根”的逆否命题;其中真命题的个数是( )
A、0个 B、1个 C、2个 D、3个5. 已知 , 则“ 且 ”是“抛物线 的焦点在 轴非负半轴上”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件6. 下列命题正确的是( )A、 是向量
是向量  ,
,  不共线的充要条件
B、在空间四边形
不共线的充要条件
B、在空间四边形  中,
中,  C、在棱长为1的正四面体
C、在棱长为1的正四面体  中,
中,  D、设 A ,
D、设 A , 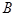 , C 三点不共线, 为平面 ABC 外一点,若
, C 三点不共线, 为平面 ABC 外一点,若  ,则
,则  , A ,
, A , 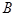 , C 四点共面
7. 若椭圆 与双曲线 有公共的焦点 , ,点 是两条曲线的交点, ,椭圆的离心率为 ,双曲线的离心率为 ,且 ,则 ( )A、 B、 C、 D、
, C 四点共面
7. 若椭圆 与双曲线 有公共的焦点 , ,点 是两条曲线的交点, ,椭圆的离心率为 ,双曲线的离心率为 ,且 ,则 ( )A、 B、 C、 D、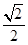 8. 已知 为双曲线 右支上一点, 为其左顶点, 为其右焦点,满足 , ,则点 到直线 的距离为( )A、
8. 已知 为双曲线 右支上一点, 为其左顶点, 为其右焦点,满足 , ,则点 到直线 的距离为( )A、 B、
B、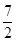 C、
C、 D、
D、 9. 如图,四边形 , , ,现将 沿 折起,当二面角 的大小在 时,直线 和 所成角为 ,则 的最大值为( )
9. 如图,四边形 , , ,现将 沿 折起,当二面角 的大小在 时,直线 和 所成角为 ,则 的最大值为( )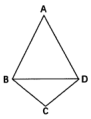 A、
A、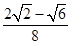 B、
B、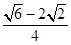 C、
C、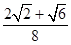 D、
D、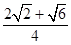 10. 若长方体 中, , , , , 分别为 , , 上的点, , , .分别记二面角 , , 的平面角为 , , ,则( )A、
10. 若长方体 中, , , , , 分别为 , , 上的点, , , .分别记二面角 , , 的平面角为 , , ,则( )A、 B、
B、 C、
C、 D、与
D、与  的值有关
的值有关
二、填空题
-
11. 双曲线 的焦点坐标是 , 渐近线方程是.12. 在空间四边形 中, , 分别是 , 的中点, 是 上一点,且 .记 ,则 , 若 , , ,且 ,则 .
 13. 设复数 ,其中 为虚数单位,则 的虚部是 , .14. 一个空间几何体的三视图如图所示,则其表面积是 , 体积是.
13. 设复数 ,其中 为虚数单位,则 的虚部是 , .14. 一个空间几何体的三视图如图所示,则其表面积是 , 体积是. 15. 已知 是抛物线 上的点,则 的最大值是.16. 已知椭圆 的左右焦点分别为 , ,动弦 过左焦点 .若 恒成立,则椭圆 的离心率的取值范围是.17. 已知矩形 中, , 为 的中点, , 交于点 , 沿着 向上翻折,使点 到 .若 在平面 上的投影 落在梯形 内部及边界上,则 的取值范围为 .
15. 已知 是抛物线 上的点,则 的最大值是.16. 已知椭圆 的左右焦点分别为 , ,动弦 过左焦点 .若 恒成立,则椭圆 的离心率的取值范围是.17. 已知矩形 中, , 为 的中点, , 交于点 , 沿着 向上翻折,使点 到 .若 在平面 上的投影 落在梯形 内部及边界上,则 的取值范围为 .
三、解答题
-
18. 已知 ,设命题 :当 时,函数 恒成立,命题 :双曲线 的离心率 .
(Ⅰ)若命题 为真命题,求实数 的取值范围;
(Ⅱ) 若命题 和 中有且只有一个真命题,求实数 的取值范围.
19. 如图,在四面体 中, , , .
(Ⅰ)求点 到平面 的距离;
(Ⅱ)求异面直线 与 所成角的大小.
20. 如图,已知多面体 中, , 平面 , , , , .
(Ⅰ)证明: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值.

