浙江省丽水市2018-2019学年高二上学期数学期末教学质量监控试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 下列直线中与直线x﹣2y+1=0平行的一条是( )A、2x﹣y+1=0 B、2x﹣4y+2=0 C、2x+4y+1=0 D、2x﹣4y+1=02. 椭圆 焦点坐标是( )A、
 B、
B、 C、
C、 D、
D、 3. 直线 被圆 所截得的弦长为( )A、 B、
3. 直线 被圆 所截得的弦长为( )A、 B、 C、
C、 D、
D、 4. 某几何体的三视图如图所示(单位: ),该几何体的体积(单位: )是( )
4. 某几何体的三视图如图所示(单位: ),该几何体的体积(单位: )是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 已知 是两条不同直线, 是不同的平面,下列命题中正确的是( )A、若
5. 已知 是两条不同直线, 是不同的平面,下列命题中正确的是( )A、若 ,
,  ,则 m∥n
B、若
,则 m∥n
B、若  ,
,  ,则
,则  C、若
C、若  ,
,  ,则
,则  D、若
D、若  ,
,  ,则
,则  6. 圆 与圆 的位置关系为( )A、内切 B、相交 C、外切 D、相离7. 斜线段 与平面 所成的角为 , 为斜足,点 是平面 上的动点且满足 ,则动点 的轨迹是( )A、直线 B、抛物线 C、椭圆 D、双曲线的一支8. 抛物线 焦点为 ,过点 作直线 交抛物线于 两点,则 的最小值为( )A、 B、
6. 圆 与圆 的位置关系为( )A、内切 B、相交 C、外切 D、相离7. 斜线段 与平面 所成的角为 , 为斜足,点 是平面 上的动点且满足 ,则动点 的轨迹是( )A、直线 B、抛物线 C、椭圆 D、双曲线的一支8. 抛物线 焦点为 ,过点 作直线 交抛物线于 两点,则 的最小值为( )A、 B、 C、
C、 D、
D、 9. 椭圆 的左焦点为 ,直线 与椭圆相交于点 ,当 的周长最大时, 的面积是( )A、
9. 椭圆 的左焦点为 ,直线 与椭圆相交于点 ,当 的周长最大时, 的面积是( )A、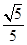 B、
B、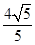 C、
C、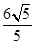 D、
D、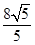 10. 如图,三棱锥 的三条棱 两两垂直, 是 的中点, 是线段 上的点, .记二面角 , , 的平面角分别为 ,则以下结论正确是( )
10. 如图,三棱锥 的三条棱 两两垂直, 是 的中点, 是线段 上的点, .记二面角 , , 的平面角分别为 ,则以下结论正确是( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 已知 为椭圆 的左顶点,该椭圆与双曲线 的渐近线在第一象限内的交点为 ,若直线 垂直于双曲线的另一条渐近线,则该双曲线的离心率为( )A、
11. 已知 为椭圆 的左顶点,该椭圆与双曲线 的渐近线在第一象限内的交点为 ,若直线 垂直于双曲线的另一条渐近线,则该双曲线的离心率为( )A、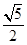 B、
B、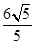 C、2
D、
12. 在棱长为1的正方体 中, 分别在棱 上,且满足 , , , 是平面 ,平面 与平面 的一个公共点,设 ,则 ( )A、 B、
C、2
D、
12. 在棱长为1的正方体 中, 分别在棱 上,且满足 , , , 是平面 ,平面 与平面 的一个公共点,设 ,则 ( )A、 B、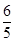 C、
C、 D、
D、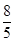
二、填空题
-
13. 已知直线经过点 ,则直线 的斜率为 , 倾斜角为 .14. 已知双曲线 ,则该双曲线的焦距为 , 渐近线方程为 .15. 若一个圆锥的底面半径是母线长的一半,侧面积和它的体积的数值相等,则该圆锥的底面半径为 , 该圆锥底面直径与母线所成角的最小值为 .16. 若实数x,y满足不等式 则 的取值范围是 .17. 我国古代数学经典名著《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马,将四个面都为直角三角形的三棱锥称为鳖臑.若三棱锥 为鳖臑,且 平面 , ,且该鳖臑的外接球的表面积为 , 则该鳖臑的表面积为 .18. 已知椭圆C: ,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则 .
19. 已知三棱锥 , ,且 , 为底面 内部及边界上的动点,则 与底面 所成角正切值的取值范围是 .三、解答题
-
20. 已知 两两垂直, , 为 的中点,点 在 上, .
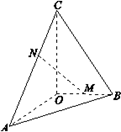
(Ⅰ)求 的长;
(Ⅱ)若点 在线段 上,设 ,当 时,求实数 的值.
