浙江省嘉兴市2018-2019学年高三上学期数学期末检测试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知复数 , ( 是虚数单位),则 ( )A、
2. 已知复数 , ( 是虚数单位),则 ( )A、 B、
B、 C、
C、 D、
D、 3. 双曲线 的离心率是( )A、 B、
3. 双曲线 的离心率是( )A、 B、 C、
C、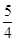 D、
D、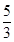 4. 某几何体的三视图如图所示(单位: ),则该几何体的体积(单位: )是( )
4. 某几何体的三视图如图所示(单位: ),则该几何体的体积(单位: )是( ) A、
A、 B、54
C、
B、54
C、 D、108
5. 已知等比数列 的各项均为正,且 , , 成等差数列,则数列 的公比是( )A、 B、2 C、 D、6. 函数 的大致图象是( )A、
D、108
5. 已知等比数列 的各项均为正,且 , , 成等差数列,则数列 的公比是( )A、 B、2 C、 D、6. 函数 的大致图象是( )A、 B、
B、 C、
C、 D、
D、 7. 已知直线 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 已知随机变量 的分布列如下,则 的最大值是( )
7. 已知直线 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 已知随机变量 的分布列如下,则 的最大值是( )-1
0
A、 B、
B、 C、
C、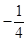 D、
D、 9. 已知长方体 的底面 为正方形, , ,且 ,侧棱 上一点 满足 ,设异面直线 与 , 与 , 与 的所成角分别为 , , ,则( )A、
9. 已知长方体 的底面 为正方形, , ,且 ,侧棱 上一点 满足 ,设异面直线 与 , 与 , 与 的所成角分别为 , , ,则( )A、 B、
B、 C、
C、 D、
D、 10. 已知向量 , 满足 , ,则 的取值范围是( )A、
10. 已知向量 , 满足 , ,则 的取值范围是( )A、 B、
B、 C、[
C、[  D、[
D、[ 
二、填空题
-
11. 计算: ,方程 的解为.12. 已知函数 的最小正周期是 ,则 , 若 ,则 .13. 已知 的展开式的所有项系数之和为27,则实数 , 展开式中含 的项的系数是.14. 在平面直角坐标系中,不等式组 所表示的平面区域的面积等于 , 的取值范围是.15. 已知正实数 , 满足 ,则 的最大值为.16. 浙江省现行的高考招生制度规定除语、数、英之外,考生须从政治、历史、地理、物理、化学、生物、技术这7门高中学考科目中选择3门作为高考选考科目,成绩计入高考总分.已知报考某高校 、 两个专业各需要一门科目满足要求即可, 专业:物理、化学、技术; 专业:历史、地理、技术.考生小李今年打算报考该高校这两个专业的选考方式有 种.(用数字作答)17. 已知点 是抛物线 上的一点,过 作直线 的垂线,垂足为 ,直线 经过原点,由 上的一点 向圆 引两条切线,分别切圆 于 , 两点,且 为直角三角形,则 的最小值是.
三、解答题
-
18. 在 中,角 , , 所对的边分别是 , , ,已知 .
(Ⅰ)求角 的大小;
(Ⅱ)若 , ,求 的面积.
19. 在数列 、 中,设 是数列 的前 项和,已知 , , , .(Ⅰ)求 和 ;
(Ⅱ)若 时, 恒成立,求整数 的最小值.

