浙江省嘉兴市2018-2019学年高一上学期数学期末检测试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 已知全集 ,则 ( )A、
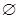 B、
B、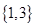 C、
C、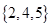 D、
D、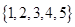 2. ( )A、 B、 C、
2. ( )A、 B、 C、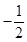 D、
D、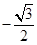 3. 下列函数中,其图像既是中心对称图形又在区间 上单调递增的是( )A、
3. 下列函数中,其图像既是中心对称图形又在区间 上单调递增的是( )A、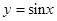 B、
B、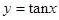 C、
C、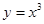 D、
D、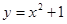 4. 设函数 ,则 ( )A、0 B、2 C、
4. 设函数 ,则 ( )A、0 B、2 C、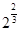 D、1
5. 已知平面上 三点不共线, 是不同于 的任意一点,若 ,则 是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形6. 为了得到 的图像,可以将函数 的图像向右平移 ( )个单位长度,则 的最小值为( )A、 B、
D、1
5. 已知平面上 三点不共线, 是不同于 的任意一点,若 ,则 是( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形6. 为了得到 的图像,可以将函数 的图像向右平移 ( )个单位长度,则 的最小值为( )A、 B、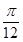 C、
C、 D、
D、 7. 如图,在 中, , ,若 ,则 ( )
7. 如图,在 中, , ,若 ,则 ( ) A、 B、 C、3 D、8. 函数 在区间 上的值域为( )A、
A、 B、 C、3 D、8. 函数 在区间 上的值域为( )A、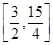 B、
B、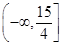 C、
C、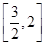 D、
D、 9. 如图,已知矩形 中, , ,该矩形所在的平面内一点 满足 ,记 , , ,则( )
9. 如图,已知矩形 中, , ,该矩形所在的平面内一点 满足 ,记 , , ,则( )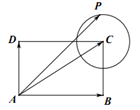 A、存在点 P ,使得
A、存在点 P ,使得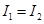 B、存在点 P ,使得
B、存在点 P ,使得  C、对任意的点 P ,有
C、对任意的点 P ,有 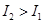 D、对任意的点 P ,有
D、对任意的点 P ,有 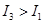 10. 存在函数 满足对任意 都有( )A、
10. 存在函数 满足对任意 都有( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 16/17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急,约翰 纳皮尔正是在研究天文学的过程中,为了简化其中的计算而发明了对数.后来天才数学家欧拉发现了对数与指数的关系,即 .
现在已知 , ,则 .
12. 已知集合 , ,则 .13. 在平面直角坐标系中,角 的顶点与原点重合,始边与 轴的非负半轴重合,终边过点 ,则 .14. 已知 、 是同一平面内两个互相垂直的单位向量,且 , , ,如果 三点共线,则实数 的值为 .15. 已知 是定义在 上的奇函数,当 时, ,若 ,求实数 的取值范围 .
16. 已知 ,则 的值是 .17. 已知平面向量 , , , , ,若向量 满足 ,则 的最大值为 .18. 函数 ,若函数 图像与直线 有两个不同的交点,求 的取值范围 .三、解答题