浙江省“温州十校联合体”2018-2019学年高二上学期数学期末考试试卷
试卷更新日期:2019-03-05 类型:期末考试
一、单选题
-
1. 直线 的倾斜角是( )A、
 B、
B、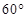 C、
C、 D、
D、 2. 抛物线 的焦点坐标是( )A、
2. 抛物线 的焦点坐标是( )A、 B、
B、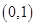 C、
C、 D、
D、 3. 设 是两条不同的直线, 是一个平面,则下列命题正确的是 ( )A、若
3. 设 是两条不同的直线, 是一个平面,则下列命题正确的是 ( )A、若 ,则
,则  B、若
B、若  ,则
,则  C、若
C、若  ,则
,则  D、若
D、若  ,则
,则  4. “直线y=x+b与圆x2+y2=1相交”是“0<b<1”的( )
4. “直线y=x+b与圆x2+y2=1相交”是“0<b<1”的( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 圆 与圆 的公切线条数为( )A、1 B、2 C、3 D、46. 双曲线 的左、右焦点分别为 , ,在左支上过点 的弦AB的长为5,那么 的周长是A、12 B、16 C、21 D、267. 已知正四棱柱 中, ,E为 中点,则异面直线BE与 所成角的余弦值为( )A、 B、
B、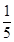 C、
C、 D、
D、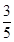 8. 如图,在正方体 中, 是侧面 内一动点,若 到直线 与直线 的距离相等,则动点 的轨迹是( )
8. 如图,在正方体 中, 是侧面 内一动点,若 到直线 与直线 的距离相等,则动点 的轨迹是( ) A、直线 B、圆 C、双曲线 D、抛物线9. 已知点 为抛物线 上的两点, 为坐标原点,且 ,则 的面积的最小值为( )A、16 B、8 C、4 D、210. 若一个四面体的四个侧面是全等的三角形,则称这样的四面体为“完美四面体”,现给出四个不同的四面体 ,记 的三个内角分别为 , , ,其中一定不是“完美四面体”的为( )A、
A、直线 B、圆 C、双曲线 D、抛物线9. 已知点 为抛物线 上的两点, 为坐标原点,且 ,则 的面积的最小值为( )A、16 B、8 C、4 D、210. 若一个四面体的四个侧面是全等的三角形,则称这样的四面体为“完美四面体”,现给出四个不同的四面体 ,记 的三个内角分别为 , , ,其中一定不是“完美四面体”的为( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 双曲线 的焦距为 , 渐近线方程为 .12. 已知直线l:mx﹣y=1,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为 , 动直线l:mx﹣y=1被圆C:x2﹣2x+y2﹣8=0截得的最短弦长为 .13. 某几何体的三视图如图(单位: ),则该几何体的体积为 ,表面积为 .
 14. 在平面直角坐标系中,A(a,0),D(0,b),a≠0,C(0,﹣2),∠CAB=90°,D是AB的中点,当A在x轴上移动时,a与b满足的关系式为;点B的轨迹E的方程为 .15. 已知椭圆 的左焦点为F,A(﹣a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为 .16. 设E,F分别是正方体ABCD﹣A1B1C1D1的棱DC上两点,且AB=2,EF=1,给出下列四个命题:
14. 在平面直角坐标系中,A(a,0),D(0,b),a≠0,C(0,﹣2),∠CAB=90°,D是AB的中点,当A在x轴上移动时,a与b满足的关系式为;点B的轨迹E的方程为 .15. 已知椭圆 的左焦点为F,A(﹣a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为 .16. 设E,F分别是正方体ABCD﹣A1B1C1D1的棱DC上两点,且AB=2,EF=1,给出下列四个命题:①三棱锥D1﹣B1EF的体积为定值;②异面直线D1B1与EF所成的角为45°;③D1B1⊥平面B1EF;④直线D1B1与平面B1EF所成的角为60°.其中正确的命题为 .
17. 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M与两定点A、B的距离之比为λ(λ>0,λ≠1),那么点M的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:x2+y2=1和点 ,点B(1,1),M为圆O上动点,则2|MA|+|MB|的最小值为 .三、解答题
-
18. 设命题 :方程 表示双曲线;命题 :斜率为 的直线 过定点 且与抛物线 有两个不同的公共点.若 是真命题,求 的取值范围.19. 如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1 , BC的中点.
 (1)、求异面直线BP与AC1所成角的余弦值;(2)、求直线CC1与平面AQC1所成角的正弦值.20. 已知抛物线 过点 .
(1)、求异面直线BP与AC1所成角的余弦值;(2)、求直线CC1与平面AQC1所成角的正弦值.20. 已知抛物线 过点 .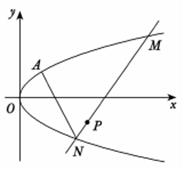 (1)、求抛物线C的方程;(2)、求过点 的直线与抛物线C交于M,N两个不同的点(均与点A不重合).设直线AM,AN的斜率分别为 , ,求证: 为定值.
(1)、求抛物线C的方程;(2)、求过点 的直线与抛物线C交于M,N两个不同的点(均与点A不重合).设直线AM,AN的斜率分别为 , ,求证: 为定值.
