黑龙江省牡丹江管理局2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2019-03-05 类型:期末考试
一、填空题
-
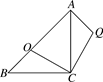
1. 袋中装有一个红球和二个黄球,它们除了颜色外都相同,随机从中摸出一球,记录下颜色后放回袋中,充分摇匀后,再随机摸出一球,两次都摸到红球的概率是。2. 关于 的一元二次方程 的一个根是0,则 的值为。3. 抛物线y=4x2-3x与y轴的交点坐标是 .4. 已知a2-5a-1=0,则5(1+2a)-2a2= .5. 如果点A(-1,4),B(m,4)在抛物线y=a(x-1)2+h上,那么m的值为.6. 如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1: .将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
 7. 如图,在平行四边形ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若弧EF的长为 ,则AB=.
7. 如图,在平行四边形ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若弧EF的长为 ,则AB=.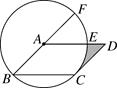 8. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为
8. 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为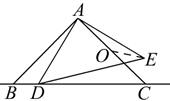 9. 某摄影小组的学生,将自己的照片向本组其他成员各赠送一张,全组共互赠了182张,若全组有x名学生,根据题意列出的方程是。10. 如图,在12×6的网格图中(每个小正方形的边长均为1个单位),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B相切,那么⊙A由图示位置需向右至少平移个单位。
9. 某摄影小组的学生,将自己的照片向本组其他成员各赠送一张,全组共互赠了182张,若全组有x名学生,根据题意列出的方程是。10. 如图,在12×6的网格图中(每个小正方形的边长均为1个单位),⊙A的半径为1,⊙B的半径为2,要使⊙A与静止的⊙B相切,那么⊙A由图示位置需向右至少平移个单位。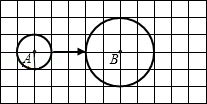
二、选择题
-
11. 下列一元二次方程中没有实数根的方程是( )A、(x-1)2=1 B、x2+2x-10=0 C、x2+4=7 D、x2+x+1=012.
已知如图①所示的四张牌,若将其中一张牌旋转180°后得到图②,则旋转的牌是( )
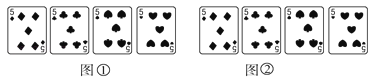 A、
A、 B、
B、 C、
C、 D、
D、 13. 在同一平面直角坐标系内,将函数y=2x2+4x-3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )A、(-3,-6) B、(1,-4) C、(1,-6) D、(-3,-4)14. 如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )
13. 在同一平面直角坐标系内,将函数y=2x2+4x-3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )A、(-3,-6) B、(1,-4) C、(1,-6) D、(-3,-4)14. 如图,O为线段AB的中点,AB=4cm,P1、P2、P3、P4到点O的距离分别是1cm、2cm、2.8cm、1.7cm,下列四点中能与A、B构成直角三角形的顶点是( )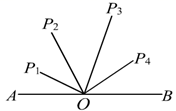 A、P1 B、P2 C、P3 D、P415. 如图,圆上有A、B、C三点,直线l与圆相切于点A,CD平分∠ACB,且与l交于点D, 若 =80°, =60°,则∠ADC的度数为( )
A、P1 B、P2 C、P3 D、P415. 如图,圆上有A、B、C三点,直线l与圆相切于点A,CD平分∠ACB,且与l交于点D, 若 =80°, =60°,则∠ADC的度数为( ) A、80° B、85° C、90° D、95°16. 有三张正面分别写有数字-2,1,3的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后把这张放回去,再从三张卡片中随机抽一张,以其正面的数字作为b的值,则点(a,b)在第一象限的概率为( )A、
A、80° B、85° C、90° D、95°16. 有三张正面分别写有数字-2,1,3的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后把这张放回去,再从三张卡片中随机抽一张,以其正面的数字作为b的值,则点(a,b)在第一象限的概率为( )A、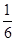 B、
B、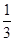 C、
C、 D、
17. 在同一直角坐标系中,函数y=ax+b和函数y=ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、
D、
17. 在同一直角坐标系中,函数y=ax+b和函数y=ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、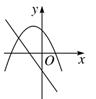 B、
B、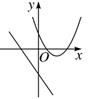 C、
C、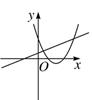 D、
D、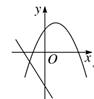 18. 若x1和x2为一元二次方程x2+2x-1=0的两个根。则x12x2+x1x22值为( )A、4 B、2 C、4 D、319. 如图,向一个半径为3m,容积为36m3的球形容器内注水,则能够反映容器内水的体积y与水深x间的函数关系的图象可能是( )
18. 若x1和x2为一元二次方程x2+2x-1=0的两个根。则x12x2+x1x22值为( )A、4 B、2 C、4 D、319. 如图,向一个半径为3m,容积为36m3的球形容器内注水,则能够反映容器内水的体积y与水深x间的函数关系的图象可能是( ) A、
A、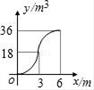 B、
B、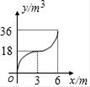 C、
C、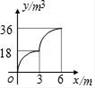 D、
D、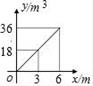 20. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(- ,y1)、点C( ,y2)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2 , 且x1<x2 , 则x1<-1<5<x2.其中正确的结论有( )
20. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(- ,y1)、点C( ,y2)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2 , 且x1<x2 , 则x1<-1<5<x2.其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个三、解答题
-
21. 用适当的方法解下列方程:(1)、3x(x+3)=2(x+3)(2)、2x2-4x-3=0.22. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 (1)、请画出△ABC绕O点逆时针旋转90°得到△A1B1C1 , 请画出△A1B1C1(2)、在x轴上求作一点P,使△PA1C1的周长最小,并直接写出P的坐标.23. 已知抛物线y=-x2+bx+c与直线y=-x+m相交于第一象限内不同的两点A(4,n),B(1,4),
(1)、请画出△ABC绕O点逆时针旋转90°得到△A1B1C1 , 请画出△A1B1C1(2)、在x轴上求作一点P,使△PA1C1的周长最小,并直接写出P的坐标.23. 已知抛物线y=-x2+bx+c与直线y=-x+m相交于第一象限内不同的两点A(4,n),B(1,4), (1)、求此抛物线的解析式.(2)、抛物线上是否存点P,使直线OP将线段AB平分,若存在直接求出P点坐标。若不存在说明理由。24. 家庭过期药品属于“国家危险废物”处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.(1)、设计调查方式:
(1)、求此抛物线的解析式.(2)、抛物线上是否存点P,使直线OP将线段AB平分,若存在直接求出P点坐标。若不存在说明理由。24. 家庭过期药品属于“国家危险废物”处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.(1)、设计调查方式:
有下列选取样本的方法①在市中心某个居民区以家庭为单位随机抽取
②在全市医务工作者中以家庭为单位随机抽取
③在全市常住人口中以家庭为单位随机抽取.
其中最合理的一种是 . (只需填上正确答案的序号)
收集整理数据:
本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下表:
处理
方式
A
继续使用
B
直接丢弃
C
送回收点
D
搁置家中
E
卖给药贩
F
直接焚烧
所占比例
8%
51%
10%
20%
6%
5%
(2)、描述数据:
此次抽样的样本数为1000户家庭,请你绘制条形统计图描述各种处理过期药品方式的家庭数;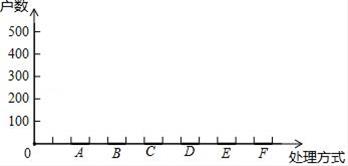 (3)、分析数据:
(3)、分析数据:
根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?
25. 某中学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.(1)、按约定,“小李同学在该天早餐得到两个油饼”是事件(填“可能”“必然”或“不可能”);(2)、请用列表或画树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.26. 如图,已知正方形ABCD的边长为 ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,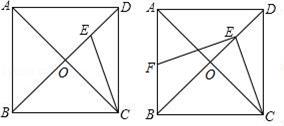 (1)、求DE的长;(2)、过点E作EF⊥CE,交AB于点F,求BF的长;27. 为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.(1)、求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);(2)、当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?28. 如图,矩形OABC在平面直角坐标系中,若x2-2 x+2=0的两根是x1、x2 , 且OC=x1+x2 , OA=x1x2
(1)、求DE的长;(2)、过点E作EF⊥CE,交AB于点F,求BF的长;27. 为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.(1)、求出利润S(元)与销售单价x(元)之间的关系式(利润=销售额﹣成本);(2)、当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?28. 如图,矩形OABC在平面直角坐标系中,若x2-2 x+2=0的两根是x1、x2 , 且OC=x1+x2 , OA=x1x2 (1)、求B点的坐标.(2)、把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BD的解析式.(3)、在平面上是否存在点P,使D、C、B、P四点形成的四边形为平形四边形?若存在,请直接写出P 点坐标;若不存在,请说明理由.
(1)、求B点的坐标.(2)、把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BD的解析式.(3)、在平面上是否存在点P,使D、C、B、P四点形成的四边形为平形四边形?若存在,请直接写出P 点坐标;若不存在,请说明理由.