黑龙江省牡丹江管理局2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-05 类型:期末考试
一、填空题
-
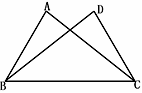
1. 某种感冒病毒的直径为0.0000000031米,用科学记数法表示为 .2. 若分式 有意义,则x的取值范围是 .3. 如图,已知AC=BD,要使△ABC≌△DCB,则只需添加一个适当的条件是.(填一个即可)
 4. 分解因式:(a-b)2-4b2= .5. 已知关于x的分式方程 有增根,则a=.6. 三角形三边长为7cm、12cm、acm,则a的取值范围是.7. 若x2+mx+4是完全平方式,则m= .8. 如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= .
4. 分解因式:(a-b)2-4b2= .5. 已知关于x的分式方程 有增根,则a=.6. 三角形三边长为7cm、12cm、acm,则a的取值范围是.7. 若x2+mx+4是完全平方式,则m= .8. 如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= . 9. 如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是.
9. 如图,已知正六边形ABCDEF的边长是5,点P是AD上的一动点,则PE+PF的最小值是.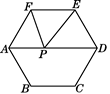 10.
10.按如下规律摆放三角形:

则第(4)堆三角形的个数为;第(n)堆三角形的个数为 .
二、选择题
-
11. 下列运算正确的是( )A、
 B、
B、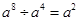 C、
C、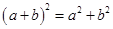 D、
12. 下列图案属于轴对称图形的是( )A、
D、
12. 下列图案属于轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 13. 一个多边形每个外角都等于36°,则这个多边形是几边形( )
13. 一个多边形每个外角都等于36°,则这个多边形是几边形( )
A、7 B、8 C、9 D、1014. 下列因式分解正确的是( )A、m2+n2=(m+n)(m-n) B、x2+2x-1=(x-1)2 C、a2-a=a(a-1) D、a2+2a+1=a(a+2)+115. 在平面直角坐标系中,已知点A(-2,a)和点B(b,-3)关于y轴对称,则ab的值是( )A、-1 B、1 C、6 D、-616. 已知 , ,则 的值为( )A、22 B、16 C、10 D、417. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=3,BD=2CD, 则BC=( )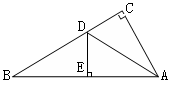 A、7 B、8 C、9 D、1018. 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=4cm,△ADC的周长为15cm,则BC的长为( )
A、7 B、8 C、9 D、1018. 如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=4cm,△ADC的周长为15cm,则BC的长为( )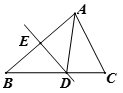 A、8cm B、11cm C、13cm D、19cm19. “五·一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每名同学比原来少摊了3元钱车费,设原来参加游览的同学共x名,则所列方程为( )A、
A、8cm B、11cm C、13cm D、19cm19. “五·一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每名同学比原来少摊了3元钱车费,设原来参加游览的同学共x名,则所列方程为( )A、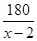 -
-  =3
B、
=3
B、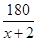 -
-  =3
C、
=3
C、 -
- 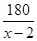 =3
D、
=3
D、 -
- 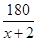 =3
20. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
=3
20. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( ) A、①②④ B、②③④ C、①②③ D、①②③④
A、①②④ B、②③④ C、①②③ D、①②③④三、简答题
-
21. 化简求值:
 ,并从0,-1,2中选一个合适的数作为a的值代入求值。 22. 如图,已知网格上最小的正方形的边长为1.
,并从0,-1,2中选一个合适的数作为a的值代入求值。 22. 如图,已知网格上最小的正方形的边长为1. (1)、分别写出A,B,C三点的坐标;(2)、作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?(3)、求△ABC的面积.23. 已知,2m= ,8n=b,m、n是正整数,求24. △ABC的三边长分别为a,b,c,且2a+ab=2c+bc,请判断△ABC是等边三角形、等腰三角形,还是直角三角形?并说明理由
(1)、分别写出A,B,C三点的坐标;(2)、作△ABC关于y轴的对称图形△A′B′C′(不写作法),想一想:关于y轴对称的两个点之间有什么关系?(3)、求△ABC的面积.23. 已知,2m= ,8n=b,m、n是正整数,求24. △ABC的三边长分别为a,b,c,且2a+ab=2c+bc,请判断△ABC是等边三角形、等腰三角形,还是直角三角形?并说明理由
25. 如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.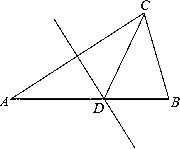 (1)、求证:△BCD是等腰三角形;(2)、△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)26. 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F。
(1)、求证:△BCD是等腰三角形;(2)、△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)26. 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F。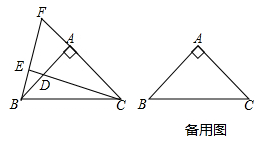 (1)、点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;(2)、点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。27. 某农场为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?28. 如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子
(1)、点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;(2)、点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请写出正确结论并证明。27. 某农场为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?28. 如图,直线MN与x轴、y轴分别相交于B、A两点,OA,OB的长满足式子 (1)、求A,B两点的坐标;(2)、若点O到AB的距离为 ,求线段AB的长;(3)、在(2)的条件下。x轴上是否存在点p使 以AB为等腰三角形,若存在,请直接写出满足条件的点p的坐标。
(1)、求A,B两点的坐标;(2)、若点O到AB的距离为 ,求线段AB的长;(3)、在(2)的条件下。x轴上是否存在点p使 以AB为等腰三角形,若存在,请直接写出满足条件的点p的坐标。