2012年浙江省义乌市中考数学试卷
试卷更新日期:2017-04-21 类型:中考真卷
一、选择题
-
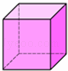
1. ﹣2的相反数是( )A、2 B、﹣2 C、±2 D、2. 下列四个立体图形中,主视图为圆的是( )A、
 B、
B、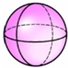 C、
C、 D、
D、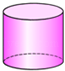 3. 下列计算正确的是( )A、a3•a2=a6 B、a2+a4=2a2 C、(a3)2=a6 D、(3a)2=a64. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间5. 在x=﹣4,﹣1,0,3中,满足不等式组 的x值是( )A、﹣4和0 B、﹣4和﹣1 C、0和3 D、﹣1和06. 如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是( )A、2 B、3 C、4 D、87. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
3. 下列计算正确的是( )A、a3•a2=a6 B、a2+a4=2a2 C、(a3)2=a6 D、(3a)2=a64. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间5. 在x=﹣4,﹣1,0,3中,满足不等式组 的x值是( )A、﹣4和0 B、﹣4和﹣1 C、0和3 D、﹣1和06. 如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是( )A、2 B、3 C、4 D、87. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )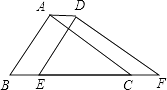 A、6 B、8 C、10 D、128. 下列计算错误的是( )A、 B、 C、 D、9. 义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是( )A、 B、 C、 D、10. 如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2 . 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=1时,y1=0,y2=4,y1<y2 , 此时M=0.下列判断:
A、6 B、8 C、10 D、128. 下列计算错误的是( )A、 B、 C、 D、9. 义乌国际小商品博览会某志愿小组有五名翻译,其中一名只会翻译阿拉伯语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是( )A、 B、 C、 D、10. 如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2 . 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 例如:当x=1时,y1=0,y2=4,y1<y2 , 此时M=0.下列判断:①当x>0时,y1>y2;
②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在;
④使得M=1的x值是﹣ 或 .
其中正确的是( )
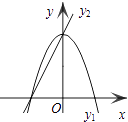 A、①② B、①④ C、②③ D、③④
A、①② B、①④ C、②③ D、③④二、填空题
-
11. 分解因式:x2﹣9= .12. 如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为 .
 13.
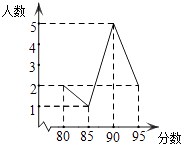
13.在义乌市中小学生“人人会乐器”演奏比赛中,某班10名学生成绩统计如图所示,则这10名学生成绩的中位数是分,众数是分.
 14. 正n边形的一个外角的度数为60°,则n的值为 .15. 近年来,义乌市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约为:11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为 .16. 如图,已知点A(0,2)、B( ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
14. 正n边形的一个外角的度数为60°,则n的值为 .15. 近年来,义乌市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约为:11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为 .16. 如图,已知点A(0,2)、B( ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: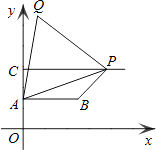 (1)、当AB为梯形的底时,点P的横坐标是;(2)、当AB为梯形的腰时,点P的横坐标是 .
(1)、当AB为梯形的底时,点P的横坐标是;(2)、当AB为梯形的腰时,点P的横坐标是 .三、解答题
-
17. 计算:|﹣2|+(﹣1)2012﹣(π﹣4)0 .
18. 如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件,使得△BDF≌△CDE,并加以证明.(不添加辅助线).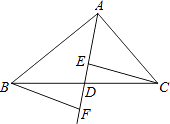 19. 学习成为商城人的时尚,义乌市新图书馆的启用,吸引了大批读者.有关部门统计了2011年10月至2012年3月期间到市图书馆的读者的职业分布情况,统计图如下:
19. 学习成为商城人的时尚,义乌市新图书馆的启用,吸引了大批读者.有关部门统计了2011年10月至2012年3月期间到市图书馆的读者的职业分布情况,统计图如下: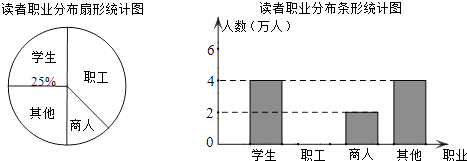 (1)、在统计的这段时间内,共有万人到市图书馆阅读,其中商人所占百分比是 ,(2)、将条形统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);(3)、若今年4月到市图书馆的读者共28000名,估计其中约有多少名职工?20. 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)、在统计的这段时间内,共有万人到市图书馆阅读,其中商人所占百分比是 ,(2)、将条形统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);(3)、若今年4月到市图书馆的读者共28000名,估计其中约有多少名职工?20. 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°. (1)、求∠ABC的度数;(2)、求证:AE是⊙O的切线;(3)、当BC=4时,求劣弧AC的长.21. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .
(1)、求∠ABC的度数;(2)、求证:AE是⊙O的切线;(3)、当BC=4时,求劣弧AC的长.21. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .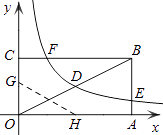 (1)、求边AB的长;(2)、求反比例函数的解析式和n的值;(3)、若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.22. 周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)、求边AB的长;(2)、求反比例函数的解析式和n的值;(3)、若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.22. 周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍. (1)、求小明骑车的速度和在甲地游玩的时间;(2)、小明从家出发多少小时后被妈妈追上?此时离家多远?(3)、若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.23. 2012•义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 .
(1)、求小明骑车的速度和在甲地游玩的时间;(2)、小明从家出发多少小时后被妈妈追上?此时离家多远?(3)、若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.23. 2012•义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 .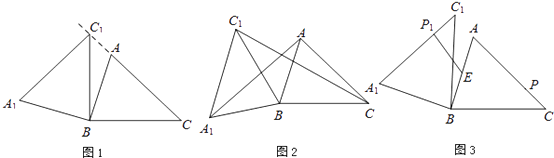 (1)、如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)、如图2,连接AA1 , CC1 . 若△ABA1的面积为4,求△CBC1的面积;(3)、如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1 , 求线段EP1长度的最大值与最小值.24. 如图1,已知直线y=kx与抛物线y= 交于点A(3,6).
(1)、如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)、如图2,连接AA1 , CC1 . 若△ABA1的面积为4,求△CBC1的面积;(3)、如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1 , 求线段EP1长度的最大值与最小值.24. 如图1,已知直线y=kx与抛物线y= 交于点A(3,6).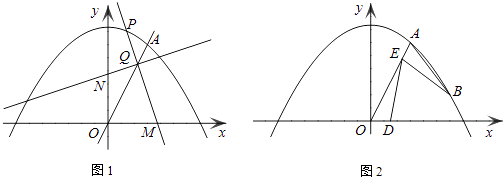 (1)、求直线y=kx的解析式和线段OA的长度;(2)、点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;(3)、如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?
(1)、求直线y=kx的解析式和线段OA的长度;(2)、点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点Q,再过点Q作直线PM的垂线,交y轴于点N.试探究:线段QM与线段QN的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;(3)、如图2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O、A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?