2012年浙江省丽水市中考数学试卷
试卷更新日期：2017-04-21 类型：中考真卷
一、选择题
-
1. 如果零上2℃记作+2℃，那么零下3℃记作（ ）A、﹣3℃ B、﹣2℃ C、+3℃ D、+2℃2. 计算3a•（2b）的结果是（ ）A、3ab B、6a C、6ab D、5ab3. 如图，数轴的单位长度为1，如果点A，B表示的数的绝对值相等，那么点A表示的数是（ ）
A、﹣4 B、﹣2 C、0 D、44. 把分式方程 转化为一元一次方程时，方程两边需同乘以（ ）A、x B、2x C、x+4 D、x（x+4）5. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（ ）
A、① B、② C、③ D、④6. 分别写有数字0，﹣1，﹣2，1，3的五张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到负数的概率是（ ）A、 B、 C、 D、7.如图，小明在操场上从A点出发，先沿南偏东30°方向走到B点，再沿南偏东60°方向走到C点．这时，∠ABC的度数是（ ）
A、120° B、135° C、150° D、160°8. 为了解中学300名男生的身高情况，随机抽取若干名男生进行身高测量，将所得数据整理后，画出频数分布直方图（如图）．估计该校男生的身高在169.5cm～174.5cm之间的人数有（ ）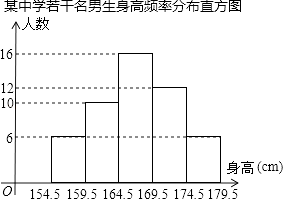
A、12 B、48 C、72 D、969. 如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是（ ）
A、① B、② C、⑤ D、⑥10.小明用棋子摆放图形来研究数的规律．图1中棋子围成三角形，其棵数3，6，9，12，…称为三角形数．类似地，图2中的4，8，12，16，…称为正方形数．下列数中既是三角形数又是正方形数的是（ ）
A、2010 B、2012 C、2014 D、2016二、填空题
-
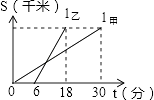
11. 写出一个比﹣3大的无理数是 ．12. 分解因式：2x2﹣8= ．13. 半径分别为3cm和4cm的两圆内切，这两圆的圆心距为 cm．14. 甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S（千米）随时间t（分）变化的函数图象，则每分钟乙比甲多行驶千米．
15. 如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是 ．
16. 如图，在直角梯形ABCD中，∠A=90°，∠B=120°，AD= ，AB=6．在底边AB上取点E，在射线DC上取点F，使得∠DEF=120°．
(1)、当点E是AB的中点时，线段DF的长度是；(2)、若射线EF经过点C，则AE的长是 ．三、解答题
-
17. 计算：2sin60°+|﹣3|﹣ ﹣ ．18. 已知A=2x+y，B=2x﹣y，计算A2﹣B2 ．19.
学校校园内有一小山坡AB，经测量，坡角∠ABC=30°，斜坡AB长为12米．为方便学生行走，决定开挖小山坡，使斜坡BD的坡比是1：3（即为CD与BC的长度之比）．A，D两点处于同一铅垂线上，求开挖后小山坡下降的高度AD．
20. 如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF于点H，交⊙O于点C，连接BD．
(1)、求证：BD平分∠ABH；(2)、如果AB=12，BC=8，求圆心O到BC的距离．21.如图，等边△OAB和等边△AFE的一边都在x轴上，双曲线y= （k＞0）经过边OB的中点C和AE的中点D．已知等边△OAB的边长为4．
(1)、求该双曲线所表示的函数解析式；(2)、求等边△AEF的边长．22. 小明参加班长竞选，需进行演讲答辩与民主测评，民主测评时一人一票，按“优秀、良好、一般”三选一投票．如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图．
(1)、求评委给小明演讲答辩分数的众数，以及民主测评为“良好”票数的扇形圆心角度数；(2)、求小明的综合得分是多少？(3)、在竞选中，小亮的民主测评得分为82分，如果他的综合得分不小于小明的综合得分，他的演讲答辩得分至少要多少分？23.在直角坐标系中，点A是抛物线y=x2在第二象限上的点，连接OA，过点O作OB⊥OA，交抛物线于点B，以OA、OB为边构造矩形AOBC．
(1)、如图1，当点A的横坐标为时，矩形AOBC是正方形；(2)、如图2，当点A的横坐标为- 时，①求点B的坐标；
②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=﹣x2 ， 试判断抛物线y=﹣x2经过平移交换后，能否经过A，B，C三点？如果可以，说出变换的过程；如果不可以，请说明理由．
24.在△ABC中，∠ABC=45°，tan∠ACB= ．如图，把△ABC的一边BC放置在x轴上，有OB=14，OC= ，AC与y轴交于点E．
(1)、求AC所在直线的函数解析式；(2)、过点O作OG⊥AC，垂足为G，求△OEG的面积；(3)、已知点F（10，0），在△ABC的边上取两点P，Q，是否存在以O，P，Q为顶点的三角形与△OFP全等，且这两个三角形在OP的异侧？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．