人教版物理必修二第五章第五节向心加速度同步训练
试卷更新日期：2015-10-21 类型：同步测试
一、选择题（共15小题）
-
1. A、B两个质点分别做匀速圆周运动，在相等时间内通过的弧长之比SA：SB=4：3，转过的圆心角之比θA：θB=3：2．则下列说法中正确的是（ ）A、它们的线速度之比vA：vB=4：3 B、它们的角速度之比ωA：ωB=2：3 C、它们的周期之比TA：TB=3：2 D、它们的向心加速度之比aA：aB=3：22. 如图所示，一个小球绕圆心O做匀速圆周运动，已知圆周半径为R ， 该小球运动的线速度大小为v ， 则它运动的向心加速度大小为（ ）
A、
B、νR
C、
D、νR2
3.如图所示为一皮带传动装置，右轮半径为r，a点在它的边缘上；左轮半径为2r，b点在它的边缘上．若在传动过程中皮带不打滑，则a点与b点的向心加速度大小之比（ ）
A、aa：ab=4：1 B、aa：ab=1：4 C、aa：ab=2：1 D、aa：ab=1：24.一质点以匀速率在水平面上做曲线运动，其轨迹如图所示．从图中可以看出，质点在a、b、c、d四点处加速度最大的点是（ ）
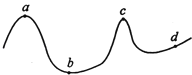A、a B、b C、c D、d5. A、B两艘快艇在湖面上做匀速圆周运动，在相同时间内，它们的路程之比为4：3，运动方向改变的角度之比为3：2，它们的向心加速度之比为（ ）A、1：2 B、2：1 C、4：2 D、3：46. 如图所示，拖拉机后轮的半径是前轮半径的两倍，A和B是前轮和后轮边缘上的点，若车行进时车轮没有打滑，则（ ）
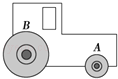A、两轮转动的周期相等 B、前轮和后轮的角速度之比为3：1 C、A点和B点的线速度大小之比为1：2 D、A点和B点的向心加速度大小之比为2：17. 图中所示为一皮带传动装置，右轮的半径范围r ， a是它边缘上的一点．左侧是一轮轴，大轮的半径为4r ， 小轮的半径为2r ， b点在小轮上，到小轮中心的距离为r ． c点和d点分别位于小轮和大轮的边缘上．若在传动过程中，皮带不打滑．则（ ）
A、a点与b点的线速度大小相等 B、a点与b点的角速度大小相等 C、b点与d点的向心加速度大小相等 D、a点与c点的线速度大小相等8. 关于做匀速圆周运动物体向心加速度的方向，下列说法正确的是（ ）A、与线速度方向始终相同 B、与线速度方向始终相反 C、始终指向圆心 D、始终保持不变9. 关于向心加速度的物理意义，下列说法正确的是（ ）A、它描述的是线速度的方向变化的快慢 B、它描述的是角速度变化的快慢 C、它描述的是线速度的大小变化的快慢 D、匀速圆周运动的向心加速度是恒定不变的10. 如图所示，为一皮带传动装置，右轮的半径为r ， a是它的边缘上的一点，左侧是一轮轴，大轮的半径为4r ， 小轮的半径为2r ， b点在小轮上，到小轮中心距离为r ， c点和d点分别位于小轮和大轮的边缘上，若在传动过程中，皮带不打滑，则（ ）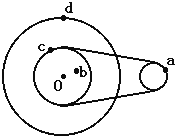
A、a点与b点线速度大小相等 B、a点与c点角速度大小相等 C、a点与d点向心加速度大小不相等 D、a、b、c、d四点，加速度最小的是b点11. 关于向心加速度，下列说法正确的是（ ）A、它是描述速度变化快慢的物理量 B、它是描述线速度大小变化快慢的物理量 C、它是描述线速度方向变化快慢的物理量 D、它是描述角速度方向变化快慢的物理量12. 关于做匀速圆周运动的物体的向心加速度，下列说法正确的是（ ）A、向心加速度大小与轨道半径成正比 B、向心加速度大小与轨道半径成反比 C、向心加速度方向与向心力方向不一致 D、向心加速度指向圆心13. 对于向心加速度的公式a=ω2r ， a=
的说法正确的是（ ） A、a与r成正比 B、a与r成反比 C、在r不变时，a与ω成正比 D、在r不变时，a与υ2成正比14. 如图所示，两个摩擦传动的轮子，A为主动轮，已知A、B轮的半径比为R1：R2=1：2，C点离圆心的距离为 ，轮子A和B通过摩擦的传动不打滑，则在两轮子做匀速圆周运动的过程中，以下关于A、B、C三点的线速度大小V、角速度大小ω、向心加速度大小a之间关系的说法正确的是（ ）
A、VA＜VB ， ωA=ωB B、aA＞aB ， ωB=ωC C、ωA＞ωB ， VB=VC D、ωA＜ωB ， VB=VC15. 荡秋千是儿童喜爱的运动，如图所示，当秋千从水平位置运动到该位置时，改变小孩的速度方向的加速度是沿（ ）
A、1方向 B、2方向 C、3方向 D、4方向二、填空题（共5小题）
-
16. 对于绕轴转动的物体，描述转动快慢的物理量有角速度ω等物理量．类似加速度，角加速度β描述角速度的变化快慢，则角加速度β的定义式是 ， 单位是 ．17.
如图所示，用皮带传动的两轮M、N半径分别是R、2R ， A为M边缘一点，B距N轮的圆心距离为R ， 则A、B两点角速度之比为 ；线速度之比为；向心加速度之比为 ．
18.如图所示，压路机后轮半径是前轮半径的3倍，A、B分别为前轮和后轮边缘上的一点，C为后轮上的一点，它离后轮轴心的距离是后轮半径的一半，则A、B、C三点的角速度之比为ωA：ωB：ωC= ， 线速度之比为vA：vB：vC= ， 向心加速度之比为aA：aB：aC= ．
19. 一物体在水平面内沿半径R=20m的圆形轨道做匀速圆周运动，线速度v=10m/s ， 那么，它的向心加速度为m/s2 ， 它的角速度为rad/s ， 它的周期为s．20.如图所示为探究质点做匀速圆周运动的向心加速度随半径变化关系实验时得到的图象，其中A为双曲线的一个分支．该实验使用了法，得到A图线是控制大小不变，研究向心加速度a与半径r的关系．得到B图线是控制 不变，研究向心加速度a与半径r的关系．
三、解答题（共5小题）
-
21.
如图所示，一个大轮通过皮带拉着小轮转动，皮带和两轮之间无滑动，大轮半径是小轮半径的两倍，大轮上的一点S与转轴的距离是半径的
，当大轮边缘上P点的向心加速度是12m/s2时，求：
(1)、大轮上的S点的向心加速度是多少？(2)、小轮上边缘处的Q点的向心加速度是多少？22.如图所示，压路机大轮的半径R是小轮半径r的2倍，压路机匀速行进时，大轮边缘上A点的向心加速度是0.12m/s2 ， 那么小轮边缘上的B点向心加速度是多少？大轮上距轴心的距离为的C点的向心加速度是多大？
23. 某走时准确的时钟，分针与时针的长度之比是1.2：1．(1)、分针与时针的角速度之比是多少？(2)、分针针尖与时针针尖的线速度之比是多少？(3)、分针和时针的运动可看做匀速圆周运动，则分针和时针转动的向心加速度之比是多少？24.如图所示，用内壁光滑的薄壁细圆管弯成的由半圆形APB（圆半径比细管的内径大得多）和直线BC组成的轨道固定在水平桌面上，已知APB部分的半径R=1.0m ， BC段长L=1.5m ． 弹射装置将一个小球（可视为质点）以v0=5m/s的水平初速度从A点弹入轨道，小球从C点离开轨道随即水平抛出，落地点D离开C的水平距离s=2.5m ， 不计空气阻力，g取10m/s2 ． 求
(1)、小球在半圆轨道上运动时的角速度ω和加速度a的大小；(2)、小球从A点运动到C点的时间t；(3)、求小球落地时的速度？
25.如图所示，甲、乙两物体自同一水平线上同时开始运动，甲沿顺时针方向做匀速圆周运动，圆半径为R；乙做自由落体运动，当乙下落至A点时，甲恰好第一次运动到最高点B ， 求甲物体匀速圆周运动的向心加速度．
