2011年浙江省义乌市中考数学试卷

试卷更新日期：2017-04-21 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣3的绝对值是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、- $\frac{1}{3}$

查看试题解析
2. 如图，DE是△ABC的中位线，若BC的长为3cm，则DE的长是（）

A、2cm B、1.5cm C、1.2cm D、1cm

查看试题解析
3. 下列运算中，正确的是（）

A、x²+x⁴=x⁶ B、2x+3y=5xy C、x⁶÷x³=x² D、（x³）²=x⁶

查看试题解析
4. 水平放置的下列几何体，主视图不是长方形的是（）

A、 B、 C、 D、

查看试题解析
5. 我市市场交易持续繁荣，市场成交额连续20年居全国各大专业市场榜首.2010年中国小商品城成交额首次突破450亿元关口．请将数据450亿元用科学记数法表示为（）（单位：元）

A、4.50×10² B、0.45×10³ C、4.50×10¹⁰ D、0.45×10¹¹

查看试题解析
6.
下列图形中，中心对称图形有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 不等式组 ${\begin{cases} 3 x + 2 > 5 \\ 5 - 2 x \geq 1 \end{cases}$ 的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
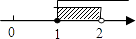8. 如图，已知AB∥CD，∠A=60°，∠C=25°，则∠E等于（）

A、60° B、25° C、35° D、45°

查看试题解析
9. 某校安排三辆车，组织九年级学生团员去敬老院参加学雷锋活动，其中小王与小菲都可以从这三辆车中任选一辆搭乘，则小王与小菲同车的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{9}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
10.
如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中：

①CE=BD；
②△ADC是等腰直角三角形；
③∠ADB=∠AEB；
④CD•AE=EF•CG；
一定正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一次函数y=2x﹣1的图象经过点（a，3），则a= ．

查看试题解析
12. 如果x₁与x₂的平均数是4，那么x₁+1与x₂+5的平均数是．

查看试题解析
13. 已知⊙O₁与⊙O₂的半径分别为3和5，且⊙O₁与⊙O₂相切，则O₁O₂等于．

查看试题解析
14. 某校为了选拔学生参加我市2011年无线电测向比赛中的装机比赛，教练对甲、乙两选手平时五次训练成绩进行统计，两选手五次训练的平均成绩均为30分钟，方差分别是S_甲²=51、S_乙²=12．则甲、乙两选手成绩比较稳定的是．

查看试题解析
15.
如图是市民广场到解百地下通道的手扶电梯示意图．其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线，∠ABC=135°，BC的长约是 $5 \sqrt{2}$ m，则乘电梯从点B到点C上升的高度h是 m．

查看试题解析
16.
如图，一次函数y=﹣2x的图象与二次函数y=﹣x²+3x图象的对称轴交于点B．

(1)、写出点B的坐标；

(2)、已知点P是二次函数y=﹣x²+3x图象在y轴右侧部分上的一个动点，将直线y=﹣2x沿y轴向上平移，分别交x轴、y轴于C、D两点．若以CD为直角边的△PCD与△OCD相似，则点P的坐标为．

查看试题解析

三、解答题

17. 计算下面各题

(1)、计算： $2011^{0} + \sqrt{8} - 2 \sin 45^{\circ}$ ；

(2)、解分式方程： $\frac{x + 3}{x - 2} = \frac{3}{2}$ ．

查看试题解析
18. 如图，已知E、F是▱ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC．

(1)、求证：△ABE≌△CDF；

(2)、请写出图中除△ABE≌△CDF外其余两对全等三角形（不再添加辅助线）．

查看试题解析
19. 商场某种商品平均每天可销售30件，每件盈利50元．为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多售出2件．设每件商品降价x元．据此规律，请回答：

(1)、商场日销售量增加件，每件商品盈利元（用含x的代数式表示）；

(2)、在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？

查看试题解析
20. 为了解某市九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段统计如下：
学业考试体育成绩（分数段）统计表
分数段
人数（人）
频率
A
48
0.2
B
a
0.25
C
84
0.35
D
36
b
E
12
0.05
分数段为：（A：50分；B：49﹣45分；C：44﹣40分；D：39﹣30分；E：29﹣0分）
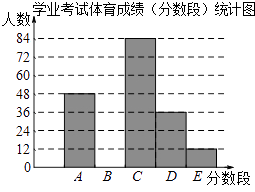
根据上面提供的信息，回答下列问题：

(1)、在统计表中，a的值为， b的值为，

(2)、将统计图补充完整（温馨提示：作图时别忘了用0.5毫米及以上的黑色签字笔涂黑）；

(3)、甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数．”请问：甲同学的体育成绩应在什么分数段内？（填相应分数段的字母）

(4)、如果把成绩在40分以上（含40分）定为优秀，那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名？

查看试题解析
21. 如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E．⊙O的切线BF与弦AD的延长线相交于点F，且AD=3，cos∠BCD= $\frac{3}{4}$ ．

(1)、求证：CD∥BF；

(2)、求⊙O的半径；

(3)、求弦CD的长．

查看试题解析
22.
如图，在直角坐标系中，O为坐标原点．已知反比例函数y= $\frac{k}{x}$ （k＞0）的图象经过点A（2，m），过点A作AB⊥x轴于点B，且△AOB的面积为 $\frac{1}{2}$ ．

(1)、求k和m的值；

(2)、点C（x，y）在反比例函数y= $\frac{k}{x}$ 的图象上，求当1≤x≤3时函数值y的取值范围；

(3)、过原点O的直线l与反比例函数y= $\frac{k}{x}$ 的图象交于P、Q两点，试根据图象直接写出线段PQ长度的最小值．

查看试题解析
23. 如图1，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点（点P与点C不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A₁B₁P，连接AA₁ ，射线AA₁分别交射线PB、射线B₁B于点E、F．

(1)、如图1，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在关系（填“相似”或“全等”），并说明理由；

(2)、如图2，设∠ABP=β．当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；

(3)、如图3，当α=60°时，点E、F与点B重合．已知AB=4，设DP=x，△A₁BB₁的面积为S，求S关于x的函数关系式．

查看试题解析
24.
已知二次函数的图象经过A（2，0）、C（0，12）两点，且对称轴为直线x=4．设顶点为点P，与x轴的另一交点为点B．

(1)、求二次函数的解析式及顶点P的坐标；

(2)、如图1，在直线 y=2x上是否存在点D，使四边形OPBD为等腰梯形？若存在，求出点D的坐标；若不存在，请说明理由；

(3)、如图2，点M是线段OP上的一个动点（O、P两点除外），以每秒 $\sqrt{2}$ 个单位长度的速度由点P向点O 运动，过点M作直线MN∥x轴，交PB于点N．将△PMN沿直线MN对折，得到△P₁MN．在动点M的运动过程中，设△P₁MN与梯形OMNB的重叠部分的面积为S，运动时间为t秒．求S关于t的函数关系式．

查看试题解析

学业考试体育成绩（分数段）统计表
分数段	人数（人）	频率
A	48	0.2
B	a	0.25
C	84	0.35
D	36	b
E	12	0.05