2011年浙江省衢州市中考数学试卷
试卷更新日期：2017-04-21 类型：中考真卷
一、选择题
-
1. ﹣2的相反数为（ ）A、2 B、 C、﹣2 D、-2. 衢州市“十二五”规划纲要指出，力争到2015年，全市农民人均年纯收入超13000元，数13000用科学记数法可以表示为（ ）A、13×103 B、1.3×104 C、0.13×104 D、130×1023. 在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：44，45，42，48，46，43，47，45．则这组数据的极差为（ ）A、2 B、4 C、6 D、84. 如图，下列几何体的俯视图是右面所示图形的是（ ）
A、
B、
C、
D、
5. 衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF、AG分别架在墙体的点B、点C处，且AB=AC，侧面四边形BDEC为矩形．若测得∠FAG=110°，则∠FBD=（ ）
A、35° B、40° C、55° D、70°6. 如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（ ）
A、1 B、2 C、3 D、47. 5月19日为中国旅游日，衢州推出“读万卷书，行万里路，游衢州景”的主题系列旅游惠民活动，市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点；下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩，则王先生恰好上午选中孔氏南宗家庙，下午选中江郎山这两个地的概率是（ ）A、 B、 C、 D、8. 一个圆形人工湖如图所示，弦AB是湖上的一座桥，已知桥AB长100m，测得圆周角∠ACB=45°，则这个人工湖的直径AD为（ ）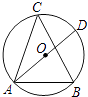
A、 B、 C、 D、9. 小亮同学骑车上学，路上要经过平路、下坡、上坡和平路（如图），若小亮上坡、平路、下坡的速度分别为v1 ， v2 ， v3 ， v1＜v2＜v3 ， 则小亮同学骑车上学时，离家的路程s与所用时间t的函数关系图象可能是（ ）
A、
B、
C、
D、
10. 如图，一张半径为1的圆形纸片在边长为a（a≥3）的正方形内任意移动，则该正方形内，这张圆形纸片“不能接触到的部分”的面积是（ ）
A、a2﹣π B、（4﹣π）a2 C、π D、4﹣π二、填空题
-
11. 方程x2﹣2x=0的解为 ．12. 如图，直尺一边AB与量角器的零刻度线CD平行，若量角器的一条刻度线OF的读数为70°，OF与AB交于点E，那么∠AEF= ．
13.在一自助夏令营活动中，小明同学从营地A出发，要到A地的北偏东60°方向的C处，他先沿正东方向走了200m到达B地，再沿北偏东30°方向走，恰能到达目的地C（如图），那么，由此可知，B、C两地相距 m．
14. 下列材料来自2006年5月衢州有关媒体的真实报道：有关部门进行民众安全感满意度调查，方法是：在全市内采用等距抽样，抽取32个小区，共960户，每户抽一名年满16周岁并能清楚表达意见的人，同时，对比前一年的调查结果，得到统计图如下：
写出2005年民众安全感满意度的众数选项是；该统计图存在一个明显的错误是 ．
15.在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB= ，反比例函数 的图象经过AO的中点C，且与AB交于点D，则点D的坐标为 ．
16. 木工师傅可以用角尺测量并计算出圆的半径r，用角尺的较短边紧靠⊙O，并使较长边与⊙O相切于点C，假设角尺的较长边足够长，角尺的顶点为B，较短边AB=8cm，若读得BC长为acm，则用含a的代数式表示r为 ．
三、解答题
-
17. 计算下列各题.(1)、计算：|﹣2|﹣（3﹣π）0+2cos45°；(2)、化简： ．18. 解不等式 ，并把解在数轴上表示出来．
19. 有足够多的长方形和正方形卡片，如下图：
(1)、如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．
这个长方形的代数意义是 ．
(2)、小明想用类似方法解释多项式乘法（a+3b）（2a+b）=2a2+7ab+3b2 ， 那么需用2号卡片张，3号卡片张．20. 研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，放回盒中，再继续．
活动结果：摸球实验活动一共做了50次，统计结果如下表：
球的颜色
无记号
有记号
红色
黄色
红色
黄色
摸到的次数
18
28
2
2
推测计算：由上述的摸球实验可推算：
(1)、盒中红球、黄球各占总球数的百分比分别是多少？(2)、盒中有红球多少个？21. 某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系，每盆植入3株时，平均单株盈利3元，以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应该植多少株？小明的解法如下：
解：设每盆花苗增加x株，则每盆花苗有（x+3）株，平均单株盈利为（3﹣0.5x）元，
由题意得（x+3）（3﹣0.5x）=10，
化简，整理得：x2﹣3x+2=0
解这个方程，得：x1=1，x2=2，
答：要使每盆的盈利达到10元，每盆应该植入4株或5株．
(1)、本题涉及的主要数量有每盆花苗株数，平均单株盈利，每盆花苗的盈利等，请写出两个不同的等量关系： ．(2)、请用一种与小明不相同的方法求解上述问题．22. 如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．
(1)、求证：AD=EC；(2)、当∠BAC=90°时，求证：四边形ADCE是菱形．23. △ABC是一张等腰直角三角形纸板，∠C=90°，AC=BC=2，
(1)、要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1），比较甲、乙两种剪法，哪种剪法所得的正方形面积大？请说明理由．(2)、图1中甲种剪法称为第1次剪取，记所得正方形面积为s1；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为s2（如图2），则s2=；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为s3 ， 继续操作下去…，则第10次剪取时，s10=；(3)、求第10次剪取后，余下的所有小三角形的面积之和．24.已知两直线l1 ， l2分别经过点A（1，0），点B（﹣3，0），并且当两直线同时相交于y正半轴的点C时，恰好有l1⊥l2 ， 经过点A、B、C的抛物线的对称轴与直线l1交于点K，如图所示．
(1)、求点C的坐标，并求出抛物线的函数解析式；(2)、抛物线的对称轴被直线l1 ， 抛物线，直线l2和x轴依次截得三条线段，问这三条线段有何数量关系？请说明理由；(3)、当直线l2绕点C旋转时，与抛物线的另一个交点为M，请找出使△MCK为等腰三角形的点M，简述理由，并写出点M的坐标．