2011年浙江省宁波市中考数学试卷

试卷更新日期：2017-04-21 类型：中考真卷

进入出卷网下载

一、选择

1. 下列各数中是正整数的是（）

A、﹣1 B、2 C、0.5 D、 $\sqrt{2}$

查看试题解析
2. 下列计算正确的是（）

A、（a²）³=a⁶ B、a²+a²=a⁴ C、（3a）•（2a）²=6a D、3a﹣a=3

查看试题解析
3. 不等式x＞1在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
4. 据宁波市统计局公布的第六次人口普查数据，本市常住人口760.57万人，其中760.57万人用科学记数法表示为（）

A、7.6057×10⁵人 B、7.6057×10⁶人 C、7.6057×10⁷人 D、0.76057×10⁷人

查看试题解析
5. 平面直角坐标系中，与点（2，﹣3）关于原点中心对称的点是（）

A、（﹣3，2） B、（3，﹣2） C、（﹣2，3） D、（2，3）

查看试题解析
6. 如图所示物体的俯视图是（）

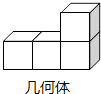A、 B、 C、 D、

查看试题解析
7. 一个多边形的内角和是720°，这个多边形的边数是（）

A、4 B、5 C、6 D、7

查看试题解析
8. 如图所示，AB∥CD，∠E=37°，∠C=20°，则∠EAB的度数为（）

A、57° B、60° C、63° D、123°

查看试题解析
9.
如图，某游乐场一山顶滑梯的高为h，滑梯的坡角为α，那么滑梯长l为（）

A、 $\frac{h}{\sin α}$ B、 $\frac{h}{\tan α}$ C、 $\frac{h}{\cos α}$ D、h•sinα

查看试题解析
10. 如图，Rt△ABC中，∠ACB=90°，AC=BC=2 $\sqrt{2}$ ，若把Rt△ABC绕边AB所在直线旋转一周，则所得几何体的表面积为（）

A、4π B、4 $\sqrt{2}$ π C、8π D、8 $\sqrt{2}$ π

查看试题解析
11. 如图，⊙O₁的半径为1，正方形ABCD的边长为6，点O₂为正方形ABCD的中心，O₁O₂垂直AB于P点，O₁O₂=8．若将⊙O₁绕点P按顺时针方向旋转360°，在旋转过程中，⊙O₁与正方形ABCD的边只有一个公共点的情况一共出现（）

A、3次 B、5次 C、6次 D、7次

查看试题解析
12.
把四张形状大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为m cm，宽为n cm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分的周长和是（）cm.

A、4m B、4n C、2（m+n） D、4（m﹣n）

查看试题解析

二、填空题

13. 实数27的立方根是．如果点P（4，﹣5）和点Q（a，b）关于原点对称，则a的值为．

查看试题解析
14. 因式分解：xy﹣y= ．

查看试题解析
15. 甲、乙、丙三位选手各10次射击成绩的平均数和方差，统计如下表：
选手
甲
乙
丙
平均数
9.3
9.3
9.3
方差
0.026
0.015
0.032
则射击成绩最稳定的选手是．（填“甲”、“乙”、“丙”中的一个）

查看试题解析
16. 抛物线y=x²的图象向上平移1个单位，则平移后的抛物线的解析式为．

查看试题解析
17. 如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，则BC= ．

查看试题解析
18.
正方形的A₁B₁P₁P₂顶点P₁、P₂在反比例函数y= $\frac{2}{x}$ （x＞0）的图象上，顶点A₁、B₁分别在x轴、y轴的正半轴上，再在其右侧作正方形P₂P₃A₂B₂ ，顶点P₃在反比例函数y= $\frac{2}{x}$ （x＞0）的图象上，顶点A₂在x轴的正半轴上，则点P₃的坐标为．

查看试题解析

三、解答题

19. 先化简，再求值：（a+2）（a﹣2）+a（1﹣a），其中a=5．

查看试题解析
20. 在一个不透明的袋子中装有3个除颜色外完全相同的小球，其中白球1个，黄球1个，红球1个，摸出一个球记下颜色后放回，再摸出一个球，请用列表法或画树状图法求两次都摸到红球的概率．

查看试题解析
21. 请在下列三个2×2的方格中，各画出一个三角形，要求所画三角形是图中三角形经过轴对称变换后得到的图形，且所画的三角形顶点与方格中的小正方形顶点重合，并将所画三角形涂上阴影．（注：所画的三个图形不能重复）

查看试题解析
22.
图①表示的是某综合商场今年1～5月的商品各月销售总额的情况，图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况，观察图①、图②，解答下列问题：

(1)、来自商场财务部的数据报告表明，商场1～5月的商品销售总额一共是410万元，请你根据这一信息将图①中的统计图补充完整；

(2)、商场服装部5月份的销售额是多少万元？

(3)、小刚观察图②后认为，5月份商场服装部的销售额比4月份减少了．你同意他的看法吗？请说明理由．

查看试题解析
23. 如图，在▱ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过点A作AG∥DB交CB的延长线于点G．

(1)、求证：DE∥BF；

(2)、若∠G=90°，求证：四边形DEBF是菱形．

查看试题解析
24. 我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．

(1)、若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？

(2)、若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？

(3)、在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．

查看试题解析
25. 阅读下面的情景对话，然后解答问题：

(1)、根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？

(2)、在Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c；

(3)、如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆 $\hat{A D B}$ 的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE．
①求证：△ACE是奇异三角形；
②当△ACE是直角三角形时，求∠AOC的度数．

查看试题解析
26.
如图，平面直角坐标系xOy中，点A的坐标为（﹣2，2），点B的坐标为（6，6），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点E．

(1)、求点E的坐标；

(2)、求抛物线的函数解析式；

(3)、点F为线段OB上的一个动点（不与点O、B重合），直线EF与抛物线交于M、N两点（点N在y轴右侧），连接ON、BN，当点F在线段OB上运动时，求△BON面积的最大值，并求出此时点N的坐标；

(4)、连接AN，当△BON面积最大时，在坐标平面内求使得△BOP与△OAN相似（点B、O、P分别与点O、A、N对应）的点P的坐标．

查看试题解析

选手	甲	乙	丙
平均数	9.3	9.3	9.3
方差	0.026	0.015	0.032