2016-2017学年浙江省杭州市大江东区八年级下学期第一次月考数学试卷

试卷更新日期：2017-04-21 类型：月考试卷

进入出卷网下载

一、仔细选一选

1. 若点P的坐标是（1，﹣2），则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{10}$ D、 $\sqrt{12}$

查看试题解析
3. 下列方程是一元二次方程的是（　　）

A、x²﹣y=1 B、x²+2x﹣3=0 C、x²+ $\frac{1}{x}$ =3 D、x﹣5y=6

查看试题解析
4. 二次根式 $\sqrt{x + 7}$ 有意义，则x的取值范围是（）

A、x≤﹣7 B、x≥﹣7 C、x＜﹣7 D、x＞﹣7

查看试题解析
5. 方程：x²﹣25=0的解是（）

A、x=5 B、x=﹣5 C、x₁=﹣5，x₂=5 D、x=±25

查看试题解析
6. 若a＜b，则下列各式中一定正确的是（）

A、a﹣b＞0 B、﹣a＞﹣b C、a+2＞b+2 D、ac＜bc

查看试题解析
7. 方程x²﹣8x+15=0左边配成一个完全平方式后，所得的方程是（）

A、（x﹣6）²=1 B、（x﹣4）²=1 C、（x﹣4）²=31 D、（x﹣4）²=﹣7

查看试题解析
8. 下列一元二次方程有两个相等实数根的是（）

A、2x²﹣x﹣1=0 B、x²﹣4x+4=0 C、4x²﹣2x﹣3=0 D、x²+6x=0

查看试题解析
9. 根据下列表格中关于x的代数式ax²+bx+c的值与x的对应值，判断方程ax²+bx+c=0（a≠0，a，b，c为常数）的一个解的范围是（）
x
5.12
5.13
5.14
5.15
ax²+bx+c
﹣0.04
﹣0.02
0.01
0.03

A、5.14＜x＜5.15 B、5.13＜x＜5.14 C、5.12＜x＜5.13 D、5.10＜x＜5.12

查看试题解析
10. 我们已经学习了利用配方法解一元二次方程，其实配方法还有其它重要应用．
例：已知x可取任何实数，试求二次三项式2x²﹣12x+14的值的范围．
解：2x²﹣12x+14=2（x²﹣6x）+14=2（x²﹣6x+3²﹣3²）+14
=2[（x﹣3）²﹣9]+14=2（x﹣3）²﹣18+14=2（x﹣3）²﹣4．
∵无论x取何实数，总有（x﹣3）²≥0，∴2（x﹣3）²﹣4≥﹣4．
即无论x取何实数，2x²﹣12x+14的值总是不小于﹣4的实数．
问题：已知x可取任何实数，则二次三项式﹣3x²+12x+11的最值情况是（）

A、有最大值﹣23 B、有最小值﹣23 C、有最大值23 D、有最小值23

查看试题解析

二、认真填一填

11. 计算 $\sqrt{8}$ ﹣2 $\sqrt{\frac{1}{2}}$ 的结果是．

查看试题解析
12. 一元二次方程﹣ $\frac{1}{2}$ x²+4x=3的二次项系数、一次项系数和常数项的乘积为．

查看试题解析
13. 写出方程x²﹣x﹣1=0的一个正根．

查看试题解析
14.
如图，A，B的坐标为（1，0），（0，2），若将线段AB平移至A₁B₁ ，则a﹣b的值为．

查看试题解析
15. 已知 $\sqrt{a - 3}$ +（b﹣5）²=0，那么以a、b为边长的直角三角形的第三边长为．

查看试题解析
16. 在目前的八年级数学下册第二章《一元二次方程》中新增了一节选学内容，其中有这样的知识点：如果方程ax²+bx+c=0（a≠0）的两根是x₁、x₂ ，那么x₁+x₂=﹣ $\frac{b}{a}$ ，x₁•x₂= $\frac{c}{a}$ ，则若关于x的方程x²﹣（k﹣1）x+k+1=0的两个实数根满足关系式|x₁﹣x₂|= $\sqrt{13}$ ，则k的值为．

查看试题解析

三、全面答一答

17. 计算：

(1)、 $\sqrt{3}$ + $\sqrt{27}$ ﹣ $\sqrt{12}$

(2)、3 $\sqrt{\frac{1}{3}}$ + $\sqrt{2}$ （ $\sqrt{3}$ ﹣ $\sqrt{6}$ ）+ $\sqrt{24}$ ÷ $\sqrt{8}$ ．

查看试题解析
18. 解方程：

(1)、（x﹣1）²=9

(2)、x²﹣5=4x．

查看试题解析
19. 完成下列问题：

(1)、若n（n≠0）是关于x的方程x²+mx﹣2n=0的根，求m+n的值；

(2)、已知x，y为实数，且y=2 $\sqrt{x - 5}$ +3 $\sqrt{5 - x}$ ﹣2．求2x﹣3y的值．

查看试题解析
20. 如图，方格纸中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求：

(1)、△ABC的面积；

(2)、边AC的长；

(3)、点B到AC边的距离．

查看试题解析
21. 如图，水库大坝截面的迎水坡坡比（DE与AE的长度之比）为5：3，背水坡坡比为1：2，大坝高DE=30m，坝顶宽CD=10m，求大坝的截面面积和周长．

查看试题解析
22. 某学校于“三•八”妇女节期间组织女教师到横店影视城旅游．下面是领队与旅行社导游收费标准的一段对话：
【领队】组团去横店影视城旅游每人收费是多少？
【导游】如果人数不超过30人，人均旅游费用为360元．
【领队】超过30人怎样优惠呢？
【导游】如果超过30人，每增加1人，人均旅游费用降低5元，但人均旅游费用不得低于300元．
该学校按旅行社的收费标准组团浏览横店影视城结束后，共支付给旅行社12400元．设该学校这次参加旅游的女教师共有x人．
请你根据上述信息，回答下列问题：

(1)、该学校参加旅游的女教师人数x的取值范围是；

(2)、该学校参加旅游的女教师每人实际应收费元（用含x的代数式表示）；

(3)、求该学校这次到横店影视城旅游的女教师共有多少人？

查看试题解析
23. 已知：如图，△ABC是边长为4cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：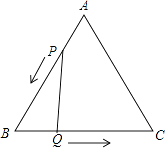

(1)、求△ABC的面积；

(2)、当t为何值是，△PBQ是直角三角形？

(3)、探究：是否存在某一时刻t，使四边形APQC的面积是△ABC面积的八分之五？如果存在，求出t的值；不存在请说明理由．

查看试题解析

x	5.12	5.13	5.14	5.15
ax²+bx+c	﹣0.04	﹣0.02	0.01	0.03