2016-2017学年辽宁省丹东市东港市八年级上学期期中数学试卷

试卷更新日期：2017-04-21 类型：期中考试

进入出卷网下载

一、选择题：

1. 若点M（a﹣4，3a﹣6）在x轴上，则点M的坐标为（）

A、（0，6） B、（2，0） C、（﹣2，0） D、（0，﹣2）

查看试题解析
2. 若5+ $\sqrt{11}$ 与5﹣ $\sqrt{11}$ 的整数部分分别为x，y，则x+y的立方根是（）

A、 $\sqrt[3]{9}$ B、± $\sqrt[3]{3}$ C、3 D、± $\sqrt[3]{9}$

查看试题解析
3.
一个长方体盒子的长、宽、高分别为15cm，10cm，20cm，点B离点C的距离是5cm，一只蚂蚁想从盒底的点A沿盒的表面爬到点B，蚂蚁爬行的最短路程是（）

A、10 $\sqrt{5}$ cm B、25cm C、5 $\sqrt{29}$ cm D、5 $\sqrt{37}$ cm

查看试题解析
4. 已知在平面直角坐标系中，点A（a﹣3，﹣5）与点B（1，b+7）关于x轴对称，则 $\sqrt{2 a - 3 b}$ 的值为（精确到0.1）（）

A、3.4 B、3.5 C、3.6 D、3.7

查看试题解析
5. 一次函数y=kx+b的图象如图所示，则关于x的方程kx+b=﹣1的解为（）

A、x=0 B、x=1 C、x= $\frac{1}{2}$ D、x=﹣2

查看试题解析
6. 如图，分别以Rt△ABC的三边为斜边向外作等腰直角三角形，若斜边AB=4，则图中阴影部分的面积为（）

A、4 B、8 C、10 D、12

查看试题解析
7. 下列说法正确的有（）（1）带根号的数都是无理数；（2）立方根等于本身的数是0和1；（3）﹣a一定没有平方根；（4）实数与数轴上的点是一一对应的；（5）两个无理数的差还是无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，数轴上A，B两点表示的数分别为﹣1，﹣ $\sqrt{2}$ ，点B关于点A的对称点为点C，则点C所表示的数是（）

A、1﹣ $\sqrt{2}$ B、 $\sqrt{2}$ ﹣1 C、2﹣ $\sqrt{2}$ D、 $\sqrt{2}$ ﹣2

查看试题解析

二、填空题：

9. $\sqrt[3]{8}$ 的平方根是．

查看试题解析
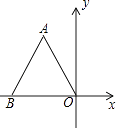
10. 已知直线a平行于y轴，且直线a上任意一点的横坐标都是3，直线b平行于x轴，且直线b与x轴的距离为2，直线a与b交点为P，则点P的坐标为．

查看试题解析
11. 已知一个直角三角形的两边长分别为3和4，则这个三角形斜边上的高为．

查看试题解析
12. 若 $\sqrt[3]{x} = \sqrt[3]{- y}$ ，则x+y= ．

查看试题解析
13. 如图，边长为4的等边△AOB在平面直角坐标系中的位置如图所示，则点A的坐标为．

查看试题解析
14. 若 $\sqrt{x - 3}$ +（y+1）⁴=0，则x^y= ．

查看试题解析
15. 若一次函数y=（m﹣3）x+1中，y值随x值的增大而减小，则m的取值需满足．

查看试题解析
16. 如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，将纸片沿AD折叠，直角边AC恰好落在斜边上，且与AE重合，则△BDE的面积为 cm² ．

查看试题解析

三、计算题

17. 计算下列小题：

(1)、 $\sqrt{\frac{1}{8}}$ + $\sqrt{18}$ ﹣ $\sqrt{8}$

(2)、（2 $\sqrt{\frac{1}{6}}$ ﹣ $\sqrt{24}$ ）÷ $\sqrt{2}$ ．

查看试题解析
18. 计算下列小题：

(1)、（ $\sqrt{6}$ + $\sqrt{5}$ ）²⁰¹⁶×（ $\sqrt{5}$ ﹣ $\sqrt{6}$ ）²⁰¹⁷

(2)、（ $\sqrt{3}$ ﹣ $\sqrt{2}$ ）²+ $\sqrt{54}$ ﹣ $\sqrt{{(- 2)}^{2}}$ ．

查看试题解析
19. 如图，在正方形网格中，每个小正方形的边长都为1，△ABC在网格中的位置如图所示，△ABC的三个顶点都在格点上．

(1)、写出△ABC三个顶点的坐标；

(2)、将点A，B，C的横坐标都乘以﹣1，纵坐标不变，分别得到点A₁ ， B₁ ， C₁ ，在图中找到点A₁ ， B₁ ， C₁ ，并顺次连接A₁ ， B₁ ， C₁得到△A₁B₁C₁ ，则这两个三角形关于对称；

(3)、若以点A，C，P为顶点的三角形与△ABC全等，直接写出所有符合条件的点P的坐标．

查看试题解析

四、解答题：

20. 如图，在△ABC中，D为BC边上的一点，已知AB=13，AD=12，AC=15，BD=5，求CD的长．

查看试题解析
21. 已知：2m+2的平方根是±4；3m+n的立方根是﹣1，求：2m﹣n的算术平方根．

查看试题解析
22. 已知：点A（﹣1，0），B（0，﹣3）．

(1)、求：直线AB的表达式；

(2)、直接写出直线AB向下平移2个单位后得到的直线表达式；

(3)、求：在（2）的平移中直线AB在第三象限内扫过的图形面积．

查看试题解析
23. 如图，甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A成的距离y（千米）与甲车行驶的时间t（时）之间的关系如图所示，观察图象回答下列问题：

(1)、A，B两城相距千米；

(2)、若两车同时出发，乙车将比甲车早到小时；

(3)、乙车的速度为千米/时；乙车出发后小时两车相遇；

(4)、直接写出，当乙车出发几小时，甲、乙两车相距40千米．

查看试题解析