2016-2017学年安徽省马鞍山市八年级上学期期末数学试卷
试卷更新日期：2017-04-21 类型：期末考试
一、选择题
-
1. 在平面直角坐标系中，点P（﹣1，1）位于（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，说明它是假命题的反例可以是（ ）A、∠1=50°，∠2=40° B、∠1=50°，∠2=50° C、∠1=40°，∠2=40° D、∠1=∠2=45°3. 已知一个等腰三角形两边长之比为1：4，周长为18，则这个等腰三角形底边长为（ ）A、2 B、6 C、8 D、2或84. 小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是（ ）A、
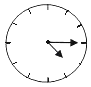B、
C、
D、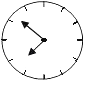
5. 下列说法中，正确的个数是（ ）①斜边和一直角边对应相等的两个直角三角形全等；
②有两边和它们的对应夹角相等的两个直角三角形全等；
③一锐角和斜边对应相等的两个直角三角形全等；
④两个锐角对应相等的两个直角三角形全等．
A、1个 B、2个 C、3个 D、4个6. 如图，直线y=﹣x+m与y=x+4的交点的横坐标为﹣2，则关于x的不等式﹣x+m＞x+4的解集为（ ）
A、x＞﹣2 B、x＜﹣2 C、x＞﹣4 D、x＜﹣47. 如图，用尺规作∠MON的平分线OP．由作图知△OAC≌△OBC，从而得OP平分∠MON，则此两个三角形全等的依据是（ ）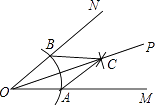
A、SAS B、ASA C、AAS D、SSS8. 已知函数y= ，则当函数值y=8时，自变量x的值是（ ）A、﹣2或4 B、4 C、﹣2 D、±2或±49. 一艘轮船在同一航线上往返于甲、乙两地．轮船先从甲地顺水航行到乙地，在乙地停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用时间为（h），航行的路程为s（km），则s与的函数图象大致是（ ）A、
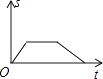B、
C、
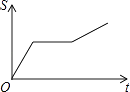D、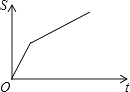
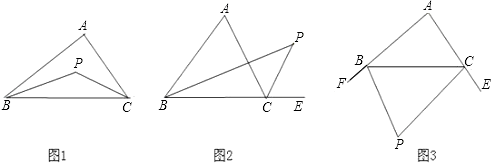
10. 已知△ABC，①如图1，若P点是∠ABC和∠ACB的角平分线的交点，则∠P=90°+ ∠A；
②如图2，若P点是∠ABC和外角∠ACE的角平分线的交点，则∠P=90°﹣∠A；
③如图3，若P点是外角∠CBF和∠BCE的角平分线的交点，则∠P=90°﹣ ∠A．
上述说法正确的个数是（ ）
A、3个 B、2个 C、1个 D、0个二、填空题
-
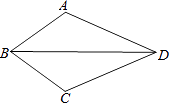
11. 已知三角形的两边分别为a=2，b=5，则第三边c的取值范围为 ．12. 函数y= 的自变量取值范围是 ．13. 将点P向下平移3个单位，向左平移2个单位后得到点Q（3，﹣1），则点P坐标为 ．14. 已知直线y=2x+（3﹣a）与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），则a的取值范围是 ．15. 如图，已知AB=BC，要使△ABD≌△CBD，还需要加一个条件，你添加的条件是 ． （只需写一个，不添加辅助线）
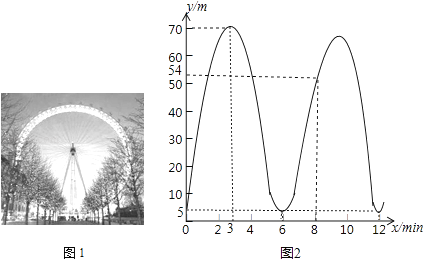
16.图中的摩天轮可抽象成一个圆，圆上一点离地面的高度y（m）与旋转时间x（min）之间的关系如图所示．根据图中的信息，摩天轮的直径为 ．
17. 如图所示，△ABC中，∠C=90°，AD平分∠BAC，AB=5，CD=2，则△ABD的面积是 ．
18. 已知在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A=度．
三、解答题
-
19. 有一块直角三角板DEF放置在△ABC上，三角板DEF的两条直角边DE、DF恰好分别经过点B、C．△ABC中，∠A=50°，求∠DBA+∠DCA的度数．
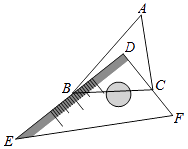20. 已知：如图，AB⊥AC，且AB=AC，AD=AE，BD=CE．求证：AD⊥AE．
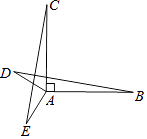21. 平面直角坐标系中，我们把点P（x，y）的横坐标与纵坐标的绝对值之和叫做点P（x，y）的勾股值，记为：「P」，即「P」=|x|+|y|．(1)、求点A（﹣1，3）的勾股值「A」；(2)、若点B在第一象限且满足「B」=3，求满足条件的所有B点与坐标轴围成的图形的面积．22. 已知：如图，AB=CD，线段AC的垂直平分线与线段BD的垂直平分线相交于点E．求证：∠ABE=∠CDE．
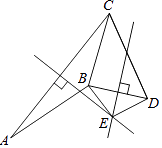23. 小明家今年种植的樱桃喜获丰收，采摘上市20天全部销售完．小明对销售情况进行跟踪记录，并将记录情况绘成图象，日销售量y（单位：千克）与上市时间 x（单位：天）的函数关系如图（1）所示，销售价格z （单位：元/千克）与上市时间x （单位：天）的函数关系式如图（2）所示．
(1)、求第10天的销售量和销售价格；(2)、试比较第10天与第12天的销售金额哪天多？24. 已知△ABC中，AC=BC，∠C=120°，点D为AB边的中点，∠EDF=60°，DE、DF分别交AC、BC于E、F点．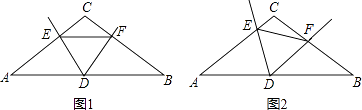
(1)、如图1，若EF∥AB．求证：DE=DF．
(2)、如图2，若EF与AB不平行． 则问题（1）的结论是否成立？说明理由．