四川省广安市、眉山市、遂宁市2018-2019学年高考文数一诊试卷
试卷更新日期:2019-03-01 类型:高考模拟
一、单选题
-
1. 若集合 2,3,4, , 4,6, ,则集合A、
 2,3,4,5,6,
2,3,4,5,6,  B、
B、 3,4,5,
3,4,5,  C、
C、 3,5,6,
3,5,6,  D、
D、 2. 复数 ( )A、
2. 复数 ( )A、 B、
B、 C、
C、 D、
D、 3. 已知平面向量 , ,且 ,则A、1 B、4 C、
3. 已知平面向量 , ,且 ,则A、1 B、4 C、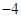 D、
4. 已知 ,则A、
D、
4. 已知 ,则A、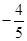 B、
B、 C、
C、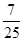 D、
5. 若双曲线 的一条渐近线为 ,则实数 ( )A、2 B、4 C、 D、6. 如图,某校一文化墙上的一幅圆形图案的半径为 分米,其内有一边长为 分米的正六边形的小孔,现向该圆形图案内随机地投入一飞镖(飞镖的大小忽略不计),则该飞镖落在圆形图案的正六边形小孔内的概率为( )
D、
5. 若双曲线 的一条渐近线为 ,则实数 ( )A、2 B、4 C、 D、6. 如图,某校一文化墙上的一幅圆形图案的半径为 分米,其内有一边长为 分米的正六边形的小孔,现向该圆形图案内随机地投入一飞镖(飞镖的大小忽略不计),则该飞镖落在圆形图案的正六边形小孔内的概率为( ) A、
A、 B、
B、 C、
D、
C、
D、 7. 下列命题错误的是( )A、不在同一直线上的三点确定一个平面 B、两两相交且不共点的三条直线确定一个平面 C、如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面 D、如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面8. 设 , , ,则a,b,c的大小关系是A、
7. 下列命题错误的是( )A、不在同一直线上的三点确定一个平面 B、两两相交且不共点的三条直线确定一个平面 C、如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面 D、如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面8. 设 , , ,则a,b,c的大小关系是A、 B、
B、 C、
C、 D、
D、 9. 已知函数 , ,要得到函数 的图象,只需将函数 的图象上的所有点( )A、横坐标缩短为原来的 ,再向左平移 个单位得到 B、横坐标缩短为原来的 ,再向左平移 个单位得到 C、横坐标伸长为原来的 2 倍,再向左平移 个单位得到 D、横坐标伸长为原来的 2 倍,再向左平移 个单位得到10. 《九章算木》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”,现有一阳马,其正视图和侧视图是如图所示的直角三角形,该“阳马”的体积为 ,若该阳马的顶点都在同一个球面上,则该球的表面积为( )
9. 已知函数 , ,要得到函数 的图象,只需将函数 的图象上的所有点( )A、横坐标缩短为原来的 ,再向左平移 个单位得到 B、横坐标缩短为原来的 ,再向左平移 个单位得到 C、横坐标伸长为原来的 2 倍,再向左平移 个单位得到 D、横坐标伸长为原来的 2 倍,再向左平移 个单位得到10. 《九章算木》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”,现有一阳马,其正视图和侧视图是如图所示的直角三角形,该“阳马”的体积为 ,若该阳马的顶点都在同一个球面上,则该球的表面积为( )

正视图 侧视图
A、 B、
B、 C、
C、 D、
D、 11. 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的 时,问一开始输入的 =( )
11. 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的 时,问一开始输入的 =( ) A、 B、 C、
A、 B、 C、 D、
D、 12. 若对 , ,有 ,函数 ,则 的值A、0 B、4 C、6 D、9
12. 若对 , ,有 ,函数 ,则 的值A、0 B、4 C、6 D、9二、填空题
-
13. 在 中,内角 , , 的对边分别为 , , ,若 , , ,则 .14. 某车间租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品8件和B类产品15件,乙种设备每天能生产A类产品10件和B类产品25件,已知设备甲每天的租赁费300元,设备乙每天的租赁费400元,现车间至少要生产A类产品100件,B类产品200件,所需租赁费最少为元
三、解答题
-
15. 已知等差数列 中, , .(1)、求数列 的通项公式;(2)、若等比数列 满足 , ,求 的前 项和 .16. 今年年初,中共中央、国务院发布《关于开展扫黑除恶专项斗争的通知》,在全国范围部署开展扫黑除恶专项斗争.那么这次的“扫黑除恶”专项斗争与2000年、2006年两次在全国范围内持续开展了十多年的“打黑除恶”专项斗争是否相同呢?某高校一个社团在年后开学后随机调查了 位该校在读大学生,就“扫黑除恶”与“打黑除恶”是否相同进行了一次调查,得到具体数据如表:
不相同
相同
合计
男
女
合计
(1)、根据如上的 列联表,能否在犯错误的概率不超过 的前提下,认为“扫黑除恶”与“打黑除恶”是否相同与性别有关"?(2)、计算这 位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率,并据此估算该校 名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数;(3)、为了解该校大学生对“扫黑除恶”与“打黑除恶”不同之处的知道情况,该校学生会组织部选取 位男生和 位女生逐个进行采访,最后再随机选取 次采访记录放到该大学的官方网站上,求最后被选取的 次采访对象中至少有一位男生的概率.参考公式: .
附表:
17. 如图,在棱长为 的正方体 中, 是线段 上的动点. (1)、证明: 平面 ;(2)、若点 是 的中点,证明:平面 平面 ;(3)、求三棱锥 的体积.18. 已知椭圆 的离心率为 ,长轴长为 ,直线 与椭圆 交于 、 两点且 为直角, 为坐标原点.(1)、求椭圆 的方程;(2)、求 的长度.
(1)、证明: 平面 ;(2)、若点 是 的中点,证明:平面 平面 ;(3)、求三棱锥 的体积.18. 已知椭圆 的离心率为 ,长轴长为 ,直线 与椭圆 交于 、 两点且 为直角, 为坐标原点.(1)、求椭圆 的方程;(2)、求 的长度.