湖南省株洲市2018-2019学年高三文数教学质量统一检测试卷(一)
试卷更新日期:2019-03-01 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知复数 满足 , 为虚数单位,则 等于( )A、
2. 已知复数 满足 , 为虚数单位,则 等于( )A、 B、
B、 C、
C、 D、
D、 3. 下列说法中,错误的是( )A、若命题 p :
3. 下列说法中,错误的是( )A、若命题 p : ,
,  ,则命题 :
,则命题 :  ,
,  B、“
B、“  ”是“
”是“  ”的必要不充分条件
C、“若
”的必要不充分条件
C、“若  ,则 a , b 中至少有一个不小于2”的逆否命题是真命题
D、函数
,则 a , b 中至少有一个不小于2”的逆否命题是真命题
D、函数  的图像关于
的图像关于 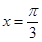 对称
4. 如下的茎叶图表示甲乙两人在5次测评中的成绩,已知甲的中位数是90,则从乙的5次测评成绩中随机抽取一次成绩,其分数高于甲的平均成绩的概率为( )
对称
4. 如下的茎叶图表示甲乙两人在5次测评中的成绩,已知甲的中位数是90,则从乙的5次测评成绩中随机抽取一次成绩,其分数高于甲的平均成绩的概率为( ) A、
A、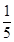 B、
B、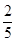 C、
C、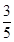 D、
5. 已知正项等比数列 的前 项和为 , 与 的等差中项为5,且 ,则 ( )A、21 B、28 C、31 D、326. 已知直线 的倾斜角为 ,则 ( )A、
D、
5. 已知正项等比数列 的前 项和为 , 与 的等差中项为5,且 ,则 ( )A、21 B、28 C、31 D、326. 已知直线 的倾斜角为 ,则 ( )A、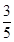 B、
C、
B、
C、 D、
D、 7. 在 中,点 为斜边 的中点, , ,则 ( )A、48 B、40 C、32 D、168. 一个几何体的三视图如图所示,则该几何体的体积为( )
7. 在 中,点 为斜边 的中点, , ,则 ( )A、48 B、40 C、32 D、168. 一个几何体的三视图如图所示,则该几何体的体积为( ) A、
A、 B、
B、 C、
C、 D、10
9. 将函数 的图像向右平移 个单位,再把所有点的横坐标伸长到原来的2倍,得到函数 的图像,则下列关于函数 的说法正确的是( )A、最小正周期为
D、10
9. 将函数 的图像向右平移 个单位,再把所有点的横坐标伸长到原来的2倍,得到函数 的图像,则下列关于函数 的说法正确的是( )A、最小正周期为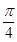 B、图像关于直线
B、图像关于直线  对称
C、图像关于点
对称
C、图像关于点  对称
D、在
对称
D、在  上是增函数
10. 过棱长为1的正方体的一条体对角线作截面,则截得正方体的截面面积的最小值是( )A、1 B、 C、 D、
上是增函数
10. 过棱长为1的正方体的一条体对角线作截面,则截得正方体的截面面积的最小值是( )A、1 B、 C、 D、 11. 双曲线 的渐近线与抛物线 相切,则该双曲线的离心率为A、 B、2 C、 D、12. 已知函数 ,若 只有一个极值点,则实数 的取值范围是( )A、
11. 双曲线 的渐近线与抛物线 相切,则该双曲线的离心率为A、 B、2 C、 D、12. 已知函数 ,若 只有一个极值点,则实数 的取值范围是( )A、 B、
B、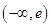 C、
C、 D、
D、
二、填空题
-
13. 已知向量 , , ,若 ,则 .14. 若 满足约束条件 ,则 的最大值为 .15. 在锐角 中,角 的对边分别为 ,已知 , , ,则 的面积为 .16. 已知 是抛物线 的焦点, 为抛物线上的动点,且 的坐标为 ,则 的最小值是 .
三、解答题
-
17. 设数列 的前 项和为 ,已知 , .(1)、求通项公式 ;(2)、设 ,求数列 的前 项和 .18. 如图,平面 平面 ,其中 为矩形, 为直角梯形, , , .
 (1)、求证:平面 平面 ;(2)、若三棱锥 体积为 ,求 与面 所成角的正弦值.19. 经过多年的努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间 内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
(1)、求证:平面 平面 ;(2)、若三棱锥 体积为 ,求 与面 所成角的正弦值.19. 经过多年的努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间 内(单位:克),统计质量的数据作出其频率分布直方图如图所示: (1)、按分层抽样的方法从质量落在 , 的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;(2)、以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
(1)、按分层抽样的方法从质量落在 , 的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;(2)、以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
参考数据: )
20. 已知 , 分别为椭圆 的左、右焦点,点 在椭圆上,且 轴, 的周长为6.(1)、求椭圆的标准方程;(2)、过点 的直线与椭圆 交于 , 两点,设 为坐标原点,是否存在常数 ,使得 恒成立?请说明理由.