湖北省鄂州市2018-2019学年高三上学期文数期中考试试卷
试卷更新日期:2019-03-01 类型:期中考试
一、单选题
-
1. 已知集合 则 ( )A、
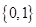 B、
B、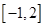 C、
C、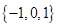 D、
D、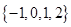 2. 等比数列 中,若 ,则 ( )A、6 B、 C、12 D、183. 计算 的结果是( )A、 B、 C、
2. 等比数列 中,若 ,则 ( )A、6 B、 C、12 D、183. 计算 的结果是( )A、 B、 C、 D、
D、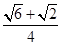 4. 下列函数为奇函数的是( )A、
4. 下列函数为奇函数的是( )A、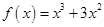 B、
B、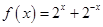 C、
C、 D、
D、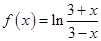 5. 已知非零向量 的夹角为 ,且 则 ( )A、
5. 已知非零向量 的夹角为 ,且 则 ( )A、 B、1
C、
D、2
6. 已知实数x,y满足约束条件 ,则 的最小值为A、1 B、
B、1
C、
D、2
6. 已知实数x,y满足约束条件 ,则 的最小值为A、1 B、 C、
D、
7. 圆 半径为 ,圆心在x轴的正半轴上,直线3x+4y+4=0与圆 相切,则圆 的方程为( )A、
C、
D、
7. 圆 半径为 ,圆心在x轴的正半轴上,直线3x+4y+4=0与圆 相切,则圆 的方程为( )A、 B、
B、 C、
C、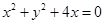 D、
D、 8. 过抛物线 的焦点 作斜率为 的直线,与抛物线在第一象限内交于点 ,若 ,则 ( )A、2 B、1 C、 D、49. 已知双曲线 过点 且其渐近线方程为 , 的顶点 恰为 的两焦点,顶点 在 上且 ,则 ( )A、 B、
8. 过抛物线 的焦点 作斜率为 的直线,与抛物线在第一象限内交于点 ,若 ,则 ( )A、2 B、1 C、 D、49. 已知双曲线 过点 且其渐近线方程为 , 的顶点 恰为 的两焦点,顶点 在 上且 ,则 ( )A、 B、 C、
C、 D、
D、 10. 若函数 有两个不同的零点,则实数 的取值范围是( )A、
10. 若函数 有两个不同的零点,则实数 的取值范围是( )A、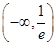 B、
B、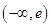 C、
C、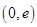 D、
D、 11. 已知数列 的前 项和为 ,首项 ,且 ,则 ( )A、
11. 已知数列 的前 项和为 ,首项 ,且 ,则 ( )A、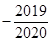 B、
B、 C、
C、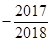 D、
D、 12. 已知双曲线 的右顶点为 , 以 为圆心的圆与双曲线 的某一条渐近线交于两点 .若 ,且 (其中 为原点),则双曲线 的离心率为( )A、
12. 已知双曲线 的右顶点为 , 以 为圆心的圆与双曲线 的某一条渐近线交于两点 .若 ,且 (其中 为原点),则双曲线 的离心率为( )A、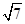 B、
B、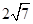 C、
C、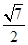 D、
D、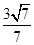
二、填空题
-
13. 函数 在点 处的切线方程为;14. 若x, ,且 ,则 的最小值为;15. 已知 , 分别是椭圆 的左、右焦点, 为椭圆 上一点,且 ,则 .16. 已知函数 满足 ,且对任意 恒有 ,则 .
三、解答题
-
17. 在 中,角 所对的边分别为 ,且 .(1)、证明: 成等比数列;(2)、若 ,且 ,求 的周长.18. 如图1,在直角 中, , 分别为 的中点,连结 并延长交 于点 ,将 沿 折起,使平面 平面 ,如图2所示.

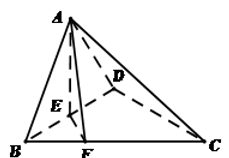
图1 图2
(1)、求证: ;(2)、求四棱锥 的体积.19. 已知数列 满足 ,数列 满足 ,且 .(Ⅰ)求 及 ;
(Ⅱ)令 ,求数列 的前 项和 .
20. 已知椭圆 的左右焦点分别为 ,且 为抛物线 的焦点, 的准线被 和圆 截得的弦长分别为 。(1)、求 方程;(2)、已知动直线 与抛物线 相切(切点异于原点),且与椭圆 相交于 两点,若椭圆 上存在点 ,使得 ,求实数 的取值范围。