2018-2019学年初中数学浙教版八年级下册4.6 反证法 同步练习
试卷更新日期：2019-03-01 类型：同步测试
一、单选题
-
1. 下列选项中，可以用来证明命题“若a2＞1，则a＞1”是假命题的反例是（ ）A、a=-2 B、a=-1 C、a= 1 D、a=22. 对于命题“已知：a∥b，b∥c，求证：a∥c”．如果用反证法，应先假设（ ）
A、a不平行b B、b不平行c C、a⊥c D、a不平行c3. 应用反证法推出矛盾的推导过程中要把下列哪些作为条件使用（ ）①结论的否定；②已知条件；③公理、定理、定义等；④原结论．
A、①② B、②③ C、①②③ D、①②④4. 命题“△ABC中，若∠A>∠B，则a>b”的结论的否定应该是（ ）A、a<b B、a≤b C、a＝b D、a≥b5. 否定“自然数a、b、c中恰有一个偶数”时的正确反设为（ ）
A、a、b、c都是奇数 B、a、b、c或都是奇数或至少有两个偶数 C、a、b、c都是偶数 D、a、b、c中至少有两个偶数6. 用反证法证明：如果AB⊥CD，AB⊥EF，那么CD∥EF．证明该命题的第一个步骤是（ ）A、假设CD∥EF B、假设AB∥EF C、假设CD和EF不平行 D、假设AB和EF不平行（ ）7. 用反证法证明命题“四边形四个内角中至少有一个角大于等于 ”，我们应该假设（ ）A、四个角都小于 B、最多有一个角大于或等于 C、有两个角小于 D、四个角都大于或等于8. 在下列各数中可以用来证明命题“质数一定是奇数”是假命题的反例是（ ）A、2 B、3 C、4 D、59.设a、b、c是互不相等的任意正数
， 
则x、y、z这三个数（ ）A、都不大于2 B、至少有一个大于2 C、都不小于2 D、至少有一个小于210. 用反证法证明“在直角三角形中，至少有一个锐角不大于45º”，应先假设这个直角三角形中（ ）A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º二、填空题
-
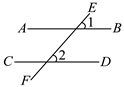
11. 如图，直线AB、CD被直线EF所截，∠1、∠2是同位角，如果∠1≠∠2，那么AB与CD不平行．用反证法证明这个命题时，应先假设：.
12. 用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：①∠A＋∠B＋∠C＝90°＋90°＋∠C>180°，这与三角形内角和为180°相矛盾，则∠A＝∠B＝90°不成立；②所以一个三角形中不能有两个直角；③假设∠A，∠B，∠C中有两个角是直角，不妨设∠A＝∠B＝90°.正确顺序的序号排列为
13. 为说明命题“如果a＞b，那么 ”是假命题，你举出的反例是 ．14. 某校九年级四个班的代表队准备举行篮球友谊赛．甲、乙、丙三位同学预测比赛的结果如下：甲说：“902班得冠军，904班得第三”；乙说：“901班得第四，903班得亚军”；丙说：“903班得第三，904班得冠军”．赛后得知，三人都只猜对了一半，则得冠军的是 ．15. 用反证法证明：两条直线被第三条直线所截，如果内错角不相等，那么这两条直线不平行已知：如图，直线a，b被直线c所截，∠1，∠2是内错角，且∠1≠∠2
求证：a不平行b.
证明：假设 ，
则（）
又∴ ∠1=∠3
∴ ∠1=∠2. 这与已知 矛盾，
∴ 不成立.
∴ .
16. 用反证法证明命题“在△ABC中，如果∠B≠∠C，那么AB≠AC．”第一步应假设三、解答题
-
17. 设a，b，c是不全相等的任意整数，若x＝a2－bc，y＝b2－ac，z＝c2－ab.求证：x，y，z中至少有一个大于零．
18.判断下列命题的真假，并给出证明（若是真命题给出证明，若是假命题举出反例）：
（1）若 ， 则a=3；
（2）如图，已知BE⊥AD，CF⊥AD，垂足分别为点E，F，且BE=CF．则AD是△ABC的中线．
19. 阅读以下证明过程：已知：在△ABC中，∠C≠90°，设AB=c，AC=b，BC=a．求证：a2+b2≠c2 ．
证明：假设a2+b2=c2 ， 则由勾股定理逆定理可知∠C=90°，这与已知中的∠C≠90°矛盾，故假设不成立，所以a2+b2≠c2 ．
请用类似的方法证明以下问题：
已知：a，b是正整数，若关于x的一元二次方程x2+2a（1﹣bx）+2b=0有两个实根x1和x2 ， 求证：x1≠x2 ．
20. （1）用反证法证明命题：“三角形的三个内角中，至少有一个内角大于或等于60°．先假设所求证的结论不成立，即 三角形内角中全都小于60° ；（2）写出命题“一次函数y=kx+b，若k＞0，b＞0，则它的图象不经过第二象限．”的逆命题，并判断逆命题的真假．若为真命题，请给予证明；若是假命题，请举反例说明．
