2018-2019学年初中数学浙教版八年级下册4.5 三角形的中位线 同步练习
试卷更新日期:2019-03-01 类型:同步测试
一、单选题
-
1. 若三角形的边长为3、4、5,那么连结各边中点所成的三角形的周长为( )
A、6 B、6.5 C、7 D、82. 在▱ABCD中,延长AB到E,使BE=AB,连结DE交BC于F,则下列结论不一定成立的是( ) A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF3. 如图,在△ABC中,延长BC至D,使得CD= BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF3. 如图,在△ABC中,延长BC至D,使得CD= BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( ) A、3 B、4 C、2 D、34. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A、3 B、4 C、2 D、34. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )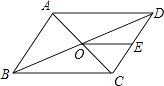 A、15 B、18 C、21 D、245. 如图所示,在 中, , , 分别是 , 的中点, , 为 上的点,连接 、 ,若 , , ,则图中阴影部分的面积为( )
A、15 B、18 C、21 D、245. 如图所示,在 中, , , 分别是 , 的中点, , 为 上的点,连接 、 ,若 , , ,则图中阴影部分的面积为( )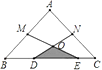 A、1cm2 B、1.5cm2 C、 2cm2 D、3cm26. 如图,在梯形 中, ,中位线 与对角线 交于 两点,若 cm, cm,则 的长等于( )
A、1cm2 B、1.5cm2 C、 2cm2 D、3cm26. 如图,在梯形 中, ,中位线 与对角线 交于 两点,若 cm, cm,则 的长等于( ) A、10 cm B、13 cm C、20 cm D、26 cm7. 如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是( )
A、10 cm B、13 cm C、20 cm D、26 cm7. 如图,△ABC的面积是12,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是( )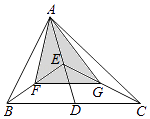 A、4.5 B、5 C、5.5 D、68. 如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB,AC的10等分点,则B1C1+B2C2+…+B9C9的值是( )
A、4.5 B、5 C、5.5 D、68. 如图,在△ABC中,BC=15,B1、B2、…B9、C1、C2、…C9分别是AB,AC的10等分点,则B1C1+B2C2+…+B9C9的值是( ) A、45 B、55 C、67.5 D、1359. 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8.以AB, BC,AC的中点A1 , B1 , C1构成△A1B1C1 , 以A1B,BB1 , A1B1的中点A2 , B2 , C2构成△A2B2C2 , ……依次操作,阴影部分面积之和将接近 ( )
A、45 B、55 C、67.5 D、1359. 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8.以AB, BC,AC的中点A1 , B1 , C1构成△A1B1C1 , 以A1B,BB1 , A1B1的中点A2 , B2 , C2构成△A2B2C2 , ……依次操作,阴影部分面积之和将接近 ( )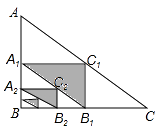 A、7 B、8 C、9 D、1010. 某地需要开辟一条隧道,隧道AB长度无法直接测量。如图所示,在地面上取一点C,使点C均可直接到达A、B两点,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )
A、7 B、8 C、9 D、1010. 某地需要开辟一条隧道,隧道AB长度无法直接测量。如图所示,在地面上取一点C,使点C均可直接到达A、B两点,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )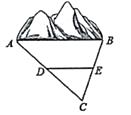 A、3300m B、2200m C、1100m D、550m
A、3300m B、2200m C、1100m D、550m二、填空题
-
11. 如图,在Rt△ABC中,∠ACB=90°,点D、点E分别是边AB、AC的中点,点F在AB上,且EF∥CD.若EF=2,则AB= .
 12. 在△ABC中,点E,F分别是边AB,AC的中点,点D在BC边上,连接DE,DF,EF,请你添加一个条件 , 使△BED与△FDE全等.
12. 在△ABC中,点E,F分别是边AB,AC的中点,点D在BC边上,连接DE,DF,EF,请你添加一个条件 , 使△BED与△FDE全等. 13. 如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1 , B1 , C1 , D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为cm.
13. 如图,四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm,点A1 , B1 , C1 , D1是四边形ABCD各边上的中点,则四边形A1B1C1D1的周长为cm. 14. 如图,在四边形 中, , , ,点 , 分别在边 , 上,点 , 分别为 , 的中点,连接 ,则 长度的最大值为 .
14. 如图,在四边形 中, , , ,点 , 分别在边 , 上,点 , 分别为 , 的中点,连接 ,则 长度的最大值为 . 15. 如图,在矩形ABCD中,AB=6,若AD=4,由作图痕迹可得GF= .
15. 如图,在矩形ABCD中,AB=6,若AD=4,由作图痕迹可得GF= . 16. 如图,已知线段AB⊥CD,E,F分别是AD,CB的中点,且AB=16,CD=12,则EF的长是.
16. 如图,已知线段AB⊥CD,E,F分别是AD,CB的中点,且AB=16,CD=12,则EF的长是.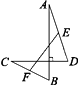
三、解答题
-
17. 如图,已知△ABC,请用圆规和直尺作出△ABC的一条中位线EF(不写作法,保留作图痕迹).
 18. 如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点,线段EF与DG之间有什么关系?为什么?
18. 如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点,线段EF与DG之间有什么关系?为什么? 19. 如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.
19. 如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值. 20. 已知:如图,点A.F,E.C在同一直线上,AB∥DC,AB=CD,∠B=∠D.
20. 已知:如图,点A.F,E.C在同一直线上,AB∥DC,AB=CD,∠B=∠D. (1)、求证:△ABE≌△CDF;(2)、若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.21. 如图,在△ABC中,AB>AC,点D在边AC上.
(1)、求证:△ABE≌△CDF;(2)、若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.21. 如图,在△ABC中,AB>AC,点D在边AC上.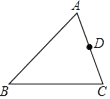 (1)、作∠ADE,使∠ADE=∠ACB,DE交AB于点E;
(1)、作∠ADE,使∠ADE=∠ACB,DE交AB于点E;(尺规作图,保留作图痕迹,不写作法)
(2)、若BC=5,点D是AC的中点,求DE的长.22. 如图, 中, ,D、E分别为AB、AC的中点,连接CD,过E作 交BC的延长线于F; (1)、求证: ;(2)、若 ,求EF的长.23. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.
(1)、求证: ;(2)、若 ,求EF的长.23. 操作与探究 探索:在如图1至图3中,△ABC的面积为a.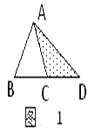

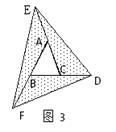

(1)、如图1,延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1 , 则S1=(用含a的代数式表示);
(2)、如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2 , 则S2=(用含a的代数式表示);(3)、在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3 , 则S3=(用含a的代数式表示).发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的倍.