2018-2019学年初中数学浙教版八年级下册4.4 平行四边形的判定 同步练习
试卷更新日期：2019-03-01 类型：同步测试
一、单选题
-
1. 下列选项中，不能判定四边形ABCD是平行四边形的是
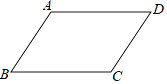A、 ， B、 ， C、 ， D、 ，2. ▱ABCD中，E，F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（ ）
A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF3. 如图，△ABC中，∠ABC＝∠BAC，D是AB的中点，EC∥AB，DE∥BC，AC与DE交于点O．下列结论中，不一定成立的是（ ）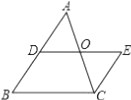
A、AC＝DE B、AB＝AC C、AD＝EC D、OA＝OE4. 已知 ABC(如图1)，按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是（ ）
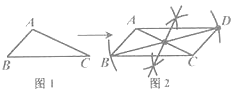A、两组对边分别平行的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、对角线互相平分的四边形是平行四边形5. 如图， ABCD中，E，F分别是AB，CD的中点，则图中有（ ）个平行四边形．
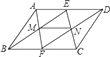A、7个 B、8个 C、9个 D、10个6. 下列命题是真命题的是（ ）A、若ac＞bc，则a＞b B、4的平方根是2 C、一组对边平行，另一组对边相等的四边形是平行四边形 D、顺次连接任意四边形各边中点所得的四边形是平行四边形7. 如图，图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（ ）
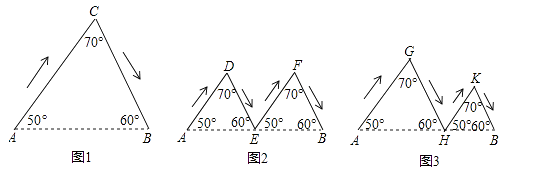A、甲＜乙＜丙 B、乙＜丙＜甲 C、丙＜乙＜甲 D、甲=乙=丙8. 如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点，增加下列条件，不能得出BE∥DF的是（ ）
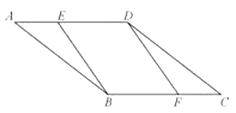A、AE=CF B、BE=DF C、∠EBF=∠FDE D、∠BED=∠BFD9. 如图是某城市部分街道的示意图，AF∥BC，EC⊥BC，AB∥DE，BD∥AE，甲、乙两人同时从B站乘车到F站，甲乘1路车，路线是B→A→E→F；乙乘2路车，路线是B→D→C→F.假定两车的速度相同，那么（ ）先到达F站．
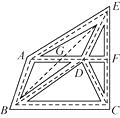A、两人同时到达F站 B、甲 C、乙 D、无法判断10. 下列图形中，一定可以拼成平行四边形的是（ ）
A、两个等腰三角形 B、两个直角三角形 C、两个锐角三角形 D、两个全等三角形二、填空题
-
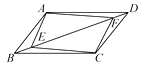
11. 如图所示，在▱ABCD中，E，F为对角线BD上的两点，要使四边形AECF为平行四边形，在不连接其他线段的前提下，还需要添加的一个条件是 ．
12. 如图，在▱ABCD中，AB=2，BC=3，∠BAD=120°，AE平分∠BAD，交BC于点E，过点C作CF∥AE，交AD于点F，则四边形AECF的面积为 ．
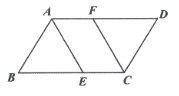13. 如图，已知在梯形ABCD中，AD∥BC，∠B=30°，∠C=75°，AD=2，BC=7，那么AB= ．
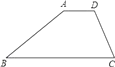14. 一个四边形的边长依次为a，b，c，d，且a2+b2+c2+d2＝2ac+2bd，则这个四边形是。15. 如图，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是。
16. 阅读下面材料：在数学课上，老师提出如下问题：
已知：如图1，△ABC及AC边的中点O．
求作：平行四边形ABCD．
小敏的作法如下：
①连接BO并延长，在延长线上截取OD=BO；
②连接DA、DC．所以四边形ABCD就是所求作的平行四边形．
老师说：“小敏的作法正确．”
请回答：小敏的作法正确的理由是 ．
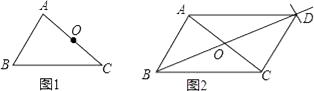
三、解答题
-
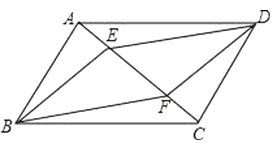
17. 已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE=CF．
求证：四边形BEDF是平行四边形．
18. 如图，在梯形ABCD中，AD∥BC，AD=24 cm，BC=30 cm，点P自点A向D以1 cm/s的速度运动，到D点即停止.点Q自点C向B以2 cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形.P，Q同时出发，几秒后其中一个四边形为平行四边形?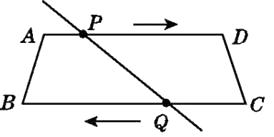
19. 一扇窗户如图1所示，窗框和窗扇用“滑块铰链”连接．如图2是图1中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，支点4处装有滑块，滑块可以左右滑动，支点B，C，D在一条直线上，延长DE交MN于点F．已知AC=DE=20cm，AE=CD=10cm，BD=40cm．
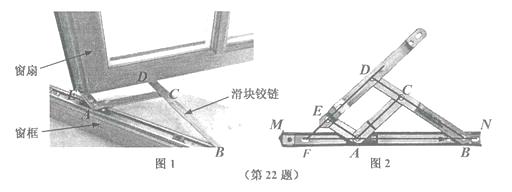(1)、当∠CAB=35 时，求窗扇与窗框的夹角∠DFB的度数．(2)、当窗扇关闭时，图中点E，A，D，C，B都在滑轨MN上．求此时点A与点B之间的距离．(3)、在(2)的前提下，将窗户推开至四边形ACDE为矩形时，求点A处的滑块移动的距离．20. 在▱ABCD中，点E在CD上，点F在AB上，连接AE、CF、DF、BE，∠DAE=∠BCF．(1)、如图1，求证：四边形DFBE是平行四边形；
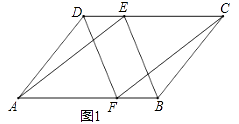(2)、如图2，若E是CD的中点，连接GH，在不添加任何辅助线的情况下，请直接写出图2中以GH为边或以GH为对角线的所有平行四边形．
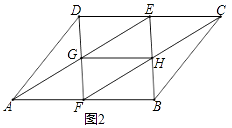21. 如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠A=∠F，∠1=∠2．
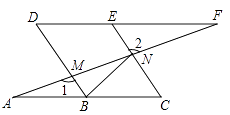(1)、求证：四边形BCED是平行四边形；(2)、已知DE=2，连接BN，若BN平分∠DBC，求CN的长．22. 如图，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD 是平行四边形，并予以证明．（写出一种即可）关系：①AD∥BC，②AB=CD，③∠A=∠C，④∠B+∠C=180°．
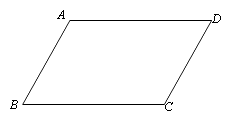
已知：在四边形ABCD中，；
求证：四边形ABCD是平行四边形．
23. 已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断① OA＝OC ② AB＝CD ③ ∠BAD＝∠DCB ④ AD∥BC
请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：
(1)、构造一个真命题，画图并给出证明；
(2)、构造一个假命题，举反例加以说明.