浙江省杭州市萧山区临浦片2016-2017学年八年级下学期期中考试数学试卷

试卷更新日期：2017-04-20 类型：期中考试

进入出卷网下载

一、选择题

1. 二次根式 $\sqrt{\frac{1}{2 x- 1}}$ 中字母x的取值范围是（）

A、x≥2 B、x＞2 C、x≥ $\frac{1}{2}$ D、x＞ $\frac{1}{2}$

查看试题解析
2. 下列方程中是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x^{2}} = 0$ B、 ${ax}^{2} +bx+c=0$ C、 $（ x- 1 ）（ x+ 2 ） = 1$ D、 $x^{2} - 2 {xy-y}^{2} = 0$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{20}$ = $2 \sqrt{10}$ B、 $\sqrt{2} • \sqrt{3} = \sqrt{6}$ C、 $\sqrt{4} - \sqrt{2} = \sqrt{2}$ D、 $\sqrt{（ - 3 ）^{2}} =- 3$

查看试题解析
4. 用配方法将方程 $x^{2} + 6 x- 11 = 0$ 变形，正确的是（）

A、(x－3）²＝20 B、（x－3）²＝2 C、（x＋3）²＝2 D、（x＋3）²＝20

查看试题解析
5. 将 $\sqrt{3^{2} \times 8}$ 化简，正确的结果是（）

A、 $6 \sqrt{2}$ B、 $\pm 6 \sqrt{2}$ C、 $3 \sqrt{8}$ D、 $\pm 3 \sqrt{8}$

查看试题解析
6. 下列性质中，平行四边形不一定具备的是（）

A、邻角互补 B、对角互补 C、对边相等 D、对角线互相平分

查看试题解析
7. 当5个整数从小到大排列，其中位数是4，如果这组数据的唯一众数是6，则5个整数的和最大是（）

A、21 B、22 C、23 D、24

查看试题解析
8. 已知关于x的方程(a－1)x²－2x+1=0有实数根，则a的取值范围是（）

A、a≤2 B、a>2 C、a≤2且a≠1 D、a<－2

查看试题解析
9. 如图，在▱ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF，CE，则下列结论：①CF=AE；②OE=OF；③DE=BF；④图中共有四对全等三角形．其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

10. 当x=-2时，二次根式 $\sqrt{2 -a}$ 的值是．

查看试题解析
11. 一个多边形的内角和等于外角和的3倍，则多边形的边数是

查看试题解析
12. 如果 $\sqrt{（ 2 a- 1 ）^{2}} = 2 a- 1$ ，则a的取值范围是 .

查看试题解析
13. 已知一组数据x₁ ， x₂ ， x₃ ，平均数和方差分别是2， $\frac{2}{3}$ ，那么另一组数据
2x₁–1，2x₂–1，2x₃–1的平均数和方差分别是，。

查看试题解析
14. 关于x的方程 $a （ x+m ）^{2} +b= 0$ 的解是x₁=－2，x₂=1（a，m，b均为常数，a≠0），则方程 $a （ x+m+ 2 ）^{2} +b= 0$ 的解是.

查看试题解析
15. 在面积为12的平行四边形ABCD中，过点A作直线BC的垂线交直线BC于点E，过点A作直线CD的垂线交直线CD于点F，若AB＝4，BC＝6，则CE＋CF的值为.

查看试题解析

三、解答题.

16. 计算：

(1)、计算： $\sqrt{8} - \sqrt{2} （ 1 + \sqrt{2} ）$ （结果保留根号）；

(2)、当 $x= 2 + \sqrt{3}$ 时，求代数式 $x^{2} - 4 x+ 2$ 的值．

查看试题解析
17. 解方程：我们已经学习了一元二次方程的多种解法：如因式分解法，开平方法，配方法和公式法，还可以运用十字相乘法，请从以下一元二次方程中任选两个，并选择你认为适当的方法解这个方程
① $x^{2} - 4 x- 1 = 0$ ② $x (2 x + 1) = 8 x - 3$
③ $x^{2} + 3 x + 1 = 0$ ④ $x^{2} - 9 = 4 (x - 3)$

查看试题解析
18.
某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：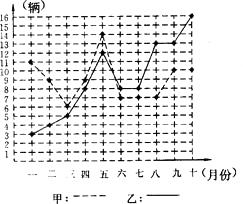

(1)、请你根据上图填写下表.
销售公司
平均数
方差
中位数
众数
甲

9
乙
9
17.0
8

(2)、请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：①从平均数和方差结合看；②从折线图上甲、乙两个汽车销售公司销售数量的趋势看（分析哪个汽车销售公司较有潜力）．

查看试题解析
19. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件.

(1)、设每件童装降价x元时，每天可销售件，每件盈利元；（用x的代数式表示

(2)、每件童装降价多少元时，平均每天赢利1200元；

(3)、要想平均每天赢利2000元，可能吗？请说明理由.

查看试题解析
20.
如图，分别延长▱ABCD的边CD，AB到E，F，使DE=BF，连接EF，分别交AD，BC于G，H，连结CG，AH.
求证：CG∥AH.

查看试题解析
21. 已知关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；

(2)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(3)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
22.
将一副三角尺如图拼接：含30°角的三角尺（△ABC）的长直角边与含45°角的三角尺（△ACD）的斜边恰好重合．已知AB＝2 $\sqrt{3}$ ，P是AC上的一个动点．

(1)、当点P运动到∠ABC的平分线上时，连接DP、BP，求CP、DP的长；

(2)、当点P在运动过程中出现PD＝BC时，求此时∠PDA的度数；

(3)、当点P运动到什么位置时，以D，P，B，Q为顶点的平行四边形的顶点Q恰好在边BC上？求出此时平行四边形的面积．

查看试题解析

销售公司	平均数	方差	中位数	众数
甲			9
乙	9	17.0		8