2011年浙江省湖州市中考数学试卷

试卷更新日期：2017-04-20 类型：中考真卷

进入出卷网下载

一、选择题

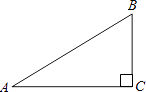
1. ﹣5的相反数是（）

A、5 B、 $\frac{1}{5}$ C、﹣5 D、- $\frac{1}{5}$

查看试题解析
2. 计算a²•a³ ，正确的结果是（）

A、2a⁶ B、2a⁵ C、a⁶ D、a⁵

查看试题解析
3. 根据全国第六次人口普查统计，湖州市常住人口约为2890000人，近似数2890000用科学记数法可表示为（）

A、2.89×10⁴ B、2.89×10⁵ C、2.89×10⁶ D、2.89×10⁷

查看试题解析
4. 如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的值为（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
5. 数据1，2，3，4，5的平均数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 下列事件中，必然事件是（）

A、掷一枚硬币，正面朝上 B、a是实数，|a|≥0 C、某运动员跳高的最好成绩是20.1米 D、从车间刚生产的产品中任意抽取一个，是次品

查看试题解析
7. 下列图形中，经过折叠不能围成一个立方体的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，已知△AOB是正三角形，OC⊥OB，OC=OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是（）

A、150° B、120° C、90° D、60°

查看试题解析
9. 如图，已知AB是⊙O的直径，C是AB延长线上一点，BC=OB，CE是⊙O的切线，切点为D，过点A作AE⊥CE，垂足为E，则CD：DE的值是（）

A、 $\frac{1}{2}$ B、1 C、2 D、3

查看试题解析
10.
如图，已知A、B是反比例函数y= $\frac{k}{x}$ （k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P纵坐标原点O出发，沿O→A→B→C匀速运动，终点为C，过点P作PM⊥x轴，PN⊥y轴，垂足分别为M、N．设四边形OMPN的面积为S，点P运动的时间为t，则S关于t的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 当x=2时，分式 $\frac{1}{x - 1}$ 的值是．

查看试题解析
12. 如图：CD平分∠ACB，DE∥AC且∠1=30°，则∠2=°．

查看试题解析
13. 某校对初三（2）班40名学生体育考试中“立定跳远”项目的得分情况进行了统计，结果如下表，
得分
10分
9分
8分
7分
6分以下
人数（人）
20
12
5
2
1
根据表中数据，若随机抽取该班的一名学生，则该学生“立定跳远”得分恰好是10分的概率是．

查看试题解析
14. 如图，已知梯形ABCD，AD∥BC，对角线AC，BD相交于点O，△AOD与△BOC的面积之比为1：9，若AD=1，则BC的长是．

查看试题解析
15. 如图，已知抛物线y=x²+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的值是．

查看试题解析
16. 如图，甲类纸片是边长为2的正方形，乙类纸片是边长为1的正方形，丙类纸片是长、宽边长分别是2和1的长方形．现有甲类纸片1张，乙类纸片4张，则应至少取丙类纸片张才能用它们拼成一个新的正方形．

查看试题解析

三、解答题

17. 计算：|﹣2|﹣2sin30°+ $\sqrt{4}$ + ${(\sqrt{2} - π)}^{0}$ ．

查看试题解析
18. 因式分解：a³﹣9a．

查看试题解析
19. 已知：一次函数y=kx+b的图象经过M（0，2），N（1，3）两点．

(1)、求k、b的值；

(2)、若一次函数y=kx+b的图象与x轴交点为A（a，0），求a的值．

查看试题解析
20. 如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，∠AOC=60°，OC=2．

(1)、求OE和CD的长；

(2)、求图中阴影部分的面积．

查看试题解析
21.
班主任张老师为了了解学生课堂发言情况，对前一天本班男、女生发言次数进行了统计，并绘制成如下频数分布折线图（图1）．

(1)、请根据图1，回答下列问题：
①这个班共有名学生，发言次数是5次的男生有人、女生有人；
②男、女生发言次数的中位数分别是次和次；

(2)、通过张老师的鼓励，第二天的发言次数比前一天明显增加，全班发言次数变化的人数的扇形统计图如图2所示，求第二天发言次数增加3次的学生人数和全班增加的发言总次数．

查看试题解析
22. 如图，已知E、F分别是▱ABCD的边BC、AD上的点，且BE=DF．

(1)、求证：四边形AECF是平行四边形；

(2)、若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长．

查看试题解析
23. 我市水产养殖专业户王大爷承包了30亩水塘，分别养殖甲鱼和桂鱼，有关成本、销售情况如下表：
养殖种类
成本（万元/亩）
销售额（万元/亩）
甲鱼
2.4
3
桂鱼
2
2.5

(1)、2010年，王大爷养殖甲鱼20亩，桂鱼10亩，求王大爷这一年共收益多少万元？（收益=销售额﹣成本）

(2)、2011年，王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70万元．若每亩养殖的成本、销售额与2010年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？

(3)、已知甲鱼每亩需要饲料500kg，桂鱼每亩需要饲料700kg，根据（2）中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍，结果运输养殖所需要全部饲料比原计划减少了2次，求王大爷原定的运输车辆每次可装载饲料多少千克？

查看试题解析
24.
如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点．P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．

(1)、求点D的坐标（用含m的代数式表示）；

(2)、当△APD是等腰三角形时，求m的值；

(3)、设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2），当点P从点O向点C运动时，点H也随之运动．请直接写出点H所经过的路径长．（不必写解答过程）

查看试题解析

养殖种类	成本（万元/亩）	销售额（万元/亩）
甲鱼	2.4	3
桂鱼	2	2.5

得分	10分	9分	8分	7分	6分以下
人数（人）	20	12	5	2	1