2017年新疆乌鲁木齐市高考数学二诊试卷（理科）

试卷更新日期：2017-04-20 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合M={x∈Z|﹣x²+3x＞0}，N={x|x²﹣4＜0}，则M∩N=（）

A、（0，2） B、（﹣2，0） C、{1，2} D、{1}

查看试题解析
2. 设复数z= $\frac{1 - 2 i}{2 - i}$ （其中i为虚数单位），则复数z在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 设f（x）= ${\begin{matrix} a^{x} ， x \geq 0 \\ \log_{a} (x^{2} + a^{2}) ， x < 0 \end{matrix}$ ，且f（2）=4，则f（﹣2）等于（）

A、1 B、2 C、3 D、4

查看试题解析
4. 某程序框图如图所示，若输出的S=26，则判断框内应填（）

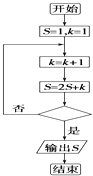A、k＞3？ B、k＞4？ C、k＞5？ D、k＞6？

查看试题解析
5. 关于直线a，b及平面α，β，下列命题中正确的是（）

A、若a∥α，α∩β=b，则a∥b B、若a∥α，b∥α，则a∥b C、若a⊥α，a∥β，则α⊥β D、若a∥α，b⊥a，则b⊥α

查看试题解析
6. 已知向量 $\vec{a} ， \vec{b}$ 满足| $\vec{a}$ |=2，| $\vec{b}$ |=1，且（ $\vec{a} + 3 \vec{b}$ ）⊥（2 $\vec{a}$ ﹣ $\vec{b}$ ），则 $\vec{a} ， \vec{b}$ 的夹角为（）

A、 $\frac{2 π}{3}$ B、 $\frac{π}{2}$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
7. 已知一个几何体的三视图如图所示（正视图是两个正方形，俯视图是两个正三角形），则其体积为（）

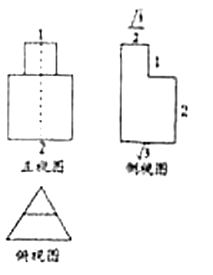A、 $\frac{3 \sqrt{3}}{2}$ B、 $\frac{9 \sqrt{3}}{4}$ C、 $3 \sqrt{3}$ D、 $\frac{9 \sqrt{3}}{2}$

查看试题解析
8. 先把函数y=sin（x+φ）的图象上个点的横坐标缩短为原来的 $\frac{1}{2}$ （纵坐标不变），再向右平移 $\frac{π}{3}$ 个单位，所得函数关于y轴对称，则φ的值可以是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、- $\frac{π}{6}$ D、- $\frac{π}{3}$

查看试题解析
9. 在△ABC中，“A＜B＜C”是“cos2A＞cos2B＞cos2C”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
10. 在△ABC中，BC=1且cosA=﹣ $\frac{\sqrt{10}}{10}$ ，B= $\frac{π}{4}$ ，则BC边上的高等于（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
11. 双曲线上存在一点与其中心及一个焦点构成等边三角形，则此双曲线的离心率为（）

A、2 B、 $\sqrt{3}$ +1 C、 $\sqrt{3}$ D、 $\sqrt{3}$ ﹣1

查看试题解析
12. 定义在R上的函数y=f（x）为减函数，且函数y=f（x﹣1）的图象关于点（1，0）对称，若f（x²﹣2x）+f（2b﹣b²）≤0，且0≤x≤2，则x﹣b的取值范围是（）

A、[﹣2，0] B、[﹣2，2] C、[0，2] D、[0，4]

查看试题解析

二、填空题

13. 二项式（ax³+ $\frac{1}{\sqrt{x}}$ ）⁷的展开式中常数项为14，则a= ．

查看试题解析
14. 若2^x+4^y=4，则x+2y的最大值是．

查看试题解析
15. 过抛物线y²=2px（p＞0）的焦点F的直线交抛物线于A，B两点，已知|AF|=3，|BF|=2，则p等于．

查看试题解析
16. 若ln（x+1）﹣1≤ax+b对任意x＞﹣1的恒成立，则 $\frac{b}{a}$ 的最小值是．

查看试题解析

三、解答题

17. 已知数列{a_n}满足a_n₊₂= ${\begin{matrix} a_{n} + 2 ， n 为奇数 \\ 3 a_{n} ， n 为偶数 \end{matrix}$ ，且a₁=1，a₂=2．

(1)、求a₃﹣a₆+a₉﹣a₁₂+a₁₅的值；

(2)、设数列{a_n}的前n项和为S_n ，当S_n＞2017时，求n的最小值．

查看试题解析
18. 如图，在多面体ABCDEF中，四边形ABCD为边长为4的正方形，M是BC的中点，EF∥平面ABCD，且EF=2，AE=DE=BF=CF= $2 \sqrt{2}$ ．

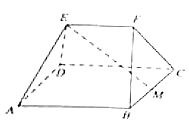(1)、求证：ME⊥平面ADE；

(2)、求二面角B﹣AE﹣D的余弦值．

查看试题解析
19. 学校某文具商店经营某种文具，商店每销售一件该文具可获利3元，若供大于求则削价处理，每处理一件文具亏损1元；若供不应求，则可以从外部调剂供应，此时每件文具仅获利2元．为了了解市场需求的情况，经销商统计了去年一年（52周）的销售情况．
销售量（件）
10
11
12
13
14
15
16
周数
2
4
8
13
13
8
4
以去年每周的销售量的频率为今年每周市场需求量的概率．

(1)、要使进货量不超过市场需求量的概率大于0.5，问进货量的最大值是多少？

(2)、如果今年的周进货量为14，写出周利润Y的分布列；

(3)、如果以周利润的期望值为考虑问题的依据，今年的周进货量定为多少合适？

查看试题解析
20. 椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率为 $\frac{\sqrt{3}}{3}$ ，过左焦点任作直线l，交椭圆的上半部分于点M，当l的斜率为 $\frac{\sqrt{3}}{3}$ 时，|FM|= $\frac{3 \sqrt{3}}{3}$ ．

(1)、求椭圆C的方程；

(2)、椭圆C上两点A，B关于直线l对称，求△AOB面积的最大值．

查看试题解析
21. 已知函数f（x）=（ax+1）e^x﹣（a+1）x﹣1．

(1)、求y=f（x）在（0，f（0））处的切线方程；

(2)、若x＞0时，不等式f（x）＞0恒成立，求a的取值范围．

查看试题解析
22. [选修4-4：坐标系与参数方程选讲]
在直角坐标系xOy中，圆C的方程为（x﹣1）²+y²= $\frac{1}{2}$ ，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点M的极坐标为（2，θ），过点M斜率为1的直线交圆C于A，B两点．

(1)、求圆C的极坐标方程；

(2)、求|MA|•|MB|的范围．

查看试题解析
23. [选修4-5：不等式选讲]
设函数f（x）=|x﹣4|，g（x）=|2x+1|．

(1)、解不等式f（x）＜g（x）；

(2)、若2f（x）+g（x）＞ax对任意的实数x恒成立，求a的取值范围．

查看试题解析

销售量（件）	10	11	12	13	14	15	16
周数	2	4	8	13	13	8	4