2017年四川省广安市、遂宁市、内江市、眉山市高考数学二诊试卷（理科）

试卷更新日期：2017-04-20 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知复数z满足z（1﹣i）²=1+i（i为虚数单位），则z=（）

A、 $\frac{1}{2}$ + $\frac{1}{2}$ i B、 $\frac{1}{2}$ ﹣ $\frac{1}{2}$ i C、﹣ $\frac{1}{2}$ + $\frac{1}{2}$ i D、﹣ $\frac{1}{2}$ ﹣ $\frac{1}{2}$ i

查看试题解析
2. 已知集合A={x|（x﹣1）²≤3x﹣3，x∈R}，B={y|y=3^x+2，x∈R}，则A∩B=（）

A、（2，+∞） B、（4，+∞） C、[2，4] D、（2，4]

查看试题解析
3. 甲、乙两类水果的质量（单位：kg）分别服从正态分布N（μ₁ ， σ₁²）及N（μ₂ ， σ₂²），其正态分布的密度曲线如图所示，则下列说法错误的是（）

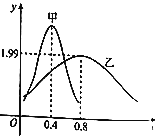A、乙类水果的质量服从的正态分布的参数σ₂=1.99 B、甲类水果的质量比乙类水果的质量更集中 C、甲类水果的平均质量μ₁=0.4kg D、甲类水果的平均质量比乙类水果的平均质量小

查看试题解析
4. 已知数列{a_n}的前n项和S_n满足S_n+S_m=S_n₊_m（n，m∈N^*）且a₁=5，则a₈=（）

A、40 B、35 C、12 D、5

查看试题解析
5. 设a=（ $\frac{5}{3}$ ） $^{\frac{1}{6}}$ ，b=（ $\frac{3}{5}$ ） $^{- \frac{1}{5}}$ ，c=ln $\frac{5}{3}$ ，则a，b，c的大小关系是（）

A、a＞b＞c B、b＞a＞c C、b＞c＞a D、a＞c＞b

查看试题解析
6. 执行如图所示的程序框图，则输出b的值为（）

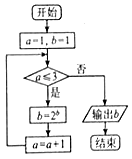A、2 B、4 C、8 D、16

查看试题解析
7. 若圆C：x²+y²﹣2x+4y=0上存在两点A，B关于直线l：y=kx﹣1对称，则k的值为（）

A、﹣1 B、﹣ $\frac{3}{2}$ C、﹣ $\frac{5}{2}$ D、﹣3

查看试题解析
8. 某同学在运动场所发现一实心椅子，其三视图如图所示（俯视图是圆的一部分及该圆的两条互相垂直的半径，有关尺寸如图，单位：m），经了解，建造该类椅子的平均成本为240元/m³ ，那么该椅子的建造成本约为（π≈3.14）（）

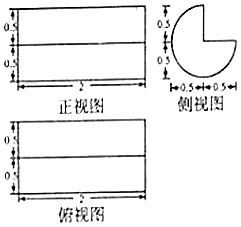A、94.20元 B、240.00元 C、282.60元 D、376.80元

查看试题解析
9. 当函数f（x）= $\sqrt{3}$ sinx+cosx﹣t（t∈R）在闭区间[0，2π]上，恰好有三个零点时，这三个零点之和为（）

A、 $\frac{10 π}{3}$ B、 $\frac{8 π}{3}$ C、 $\frac{7 π}{3}$ D、2π

查看试题解析
10. 有5位同学排成前后两排拍照，若前排站2人，则甲不站后排两端且甲、乙左右相邻的概率为（）

A、 $\frac{3}{20}$ B、 $\frac{1}{5}$ C、 $\frac{3}{10}$ D、 $\frac{3}{5}$

查看试题解析
11. 某工厂拟生产甲、乙两种实销产品．已知每件甲产品的利润为0.4万元，每件乙产品的利润为0.3万元，两种产品都需要在A，B两种设备上加工，且加工一件甲、乙产品在A，B设备上所需工时（单位：h）分别如表所示．
甲产品所需工时
乙产品所需工时
A设备
2
3
B设备
4
1
若A设备每月的工时限额为400h，B设备每月的工时限额为300h，则该厂每月生产甲、乙两种产品可获得的最大利润为（）

A、40万元 B、45万元 C、50万元 D、55万元

查看试题解析
12. 若函数g（x）满足g（g（x））=n（n∈N）有n+3个解，则称函数g（x）为“复合n+3解”函数．已知函数f（x）= ${\begin{matrix} k x + 3 ， x \leq 0 \\ \frac{e^{x - 1}}{x} ， x > 0 \end{matrix}$ （其中e是自然对数的底数，e=2.71828…，k∈R），且函数f（x）为“复合5解”函数，则k的取值范围是（）

A、（﹣∞，0） B、（﹣e，e） C、（﹣1，1） D、（0，+∞）

查看试题解析

二、填空题

13. 在Rt△ABC中，D是斜边AB的中点，若BC=6，CD=5，则 $\vec{B D} \cdot \vec{A C}$ = ．

查看试题解析
14. 有下列四个命题：

①垂直于同一条直线的两条直线平行；
②垂直于同一条直线的两个平面平行；
③垂直于同一平面的两个平面平行；
④垂直于同一平面的两条直线平行．
其中正确的命题有（填写所有正确命题的编号）．

查看试题解析
15. 若等比数列{a_n}的公比为2，且a₃﹣a₁=2 $\sqrt{3}$ ，则 $\frac{1}{a_{1}^{2}}$ + $\frac{1}{a_{2}^{2}}$ +…+ $\frac{1}{a_{n}^{2}}$ = ．

查看试题解析
16. 设抛物线C：y²=2px（p＞0）的焦点为F，点A在C上，若|AF|= $\frac{5}{2}$ ，以线段AF为直径的圆经过点B（0，1），则p= ．

查看试题解析

三、解答题

17. 在△ABC中，设内角A，B，C所对边分别为a，b，c，且sin（A﹣ $\frac{π}{6}$ ）﹣cos（A+ $\frac{5 π}{3}$ ）= $\frac{\sqrt{2}}{2}$ ．

(1)、求角A的大小；

(2)、若a= $\sqrt{5}$ ，sin²B+cos2C=1，求△ABC的面积．

查看试题解析
18. 某大学有甲、乙两个图书馆，对其借书、还书的等待时间进行调查，得到下表：
甲图书馆
借（还）书等待时间T₁（分钟）
1
2
3
4
5
频数
1500
1000
500
500
1500
乙图书馆
借（还）书等待时间T₂（分钟）
1
2
3
4
5
频数
1000
500
2000
1250
250
以表中等待时间的学生人数的频率为概率．

(1)、分别求在甲、乙两图书馆借书的平均等待时间；

(2)、学校规定借书、还书必须在同一图书馆，某学生需要借一本数学参考书，并希望借、还书的等待时间之和不超过4分钟，在哪个图书馆借、还书更能满足他的要求？

查看试题解析
19. 如图所示，在Rt△ABC中，AC⊥BC，过点C的直线VC垂直于平面ABC，D、E分别为线段VA、VC上异于端点的点．

(1)、当DE⊥平面VBC时，判断直线DE与平面ABC的位置关系，并说明理由；

(2)、当D、E、F分别为线段VA、VC、AB上的中点，且VC=2BC时，求二面角B﹣DE﹣F的余弦值．

查看试题解析
20. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）过点P（2，1），且离心率为 $\frac{\sqrt{3}}{2}$ ．
（Ⅰ）求椭圆的方程；
（Ⅱ）设O为坐标原点，在椭圆短轴上有两点M，N满足 $\vec{O M} = \vec{N O}$ ，直线PM、PN分别交椭圆于A，B．
（i）求证：直线AB过定点，并求出定点的坐标；
（ii）求△OAB面积的最大值．

查看试题解析
21. 已知函数f（x）=lnx﹣2ax（其中a∈R）．
（Ⅰ）当a=1时，求函数f（x）的图象在x=1处的切线方程；
（Ⅱ）若f（x）≤1恒成立，求a的取值范围；
（Ⅲ）设g（x）=f（x）+ $\frac{1}{2}$ x² ，且函数g（x）有极大值点x₀ ，求证：x₀f（x₀）+1+ax₀²＞0．

查看试题解析
22. [选修4-4：坐标系与参数方程]
在直角坐标系xOy中，双曲线E的参数方程为 ${\begin{matrix} x = \frac{\sqrt{3}}{\cos θ} \\ y = \tan θ \end{matrix}$ （θ为参数），设E的右焦点为F，经过第一象限的渐进线为l．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．

(1)、求直线l的极坐标方程；

(2)、设过F与l垂直的直线与y轴相交于点A，P是l上异于原点O的点，当A，O，F，P四点在同一圆上时，求这个圆的极坐标方程及点P的极坐标．

查看试题解析
23. [选修4-5：不等式选讲]
已知函数f（x）=|x+a|﹣2a，其中a∈R．

(1)、当a=﹣2时，求不等式f（x）≤2x+1的解集；

(2)、若x∈R，不等式f（x）≤|x+1|恒成立，求a的取值范围．

查看试题解析

	甲产品所需工时	乙产品所需工时
A设备	2	3
B设备	4	1

借（还）书等待时间T₁（分钟）	1	2	3	4	5
频数	1500	1000	500	500	1500

借（还）书等待时间T₂（分钟）	1	2	3	4	5
频数	1000	500	2000	1250	250