备战2019年中考数学专题一：1.3分式

试卷更新日期：2019-02-27 类型：一轮复习

进入出卷网下载

一、选择题

1. 计算 $\frac{2 x}{2 x - y} + \frac{y}{y - 2 x}$ 的结果是（）

A、1 B、﹣1 C、 D、 $x + y$

查看试题解析
2. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：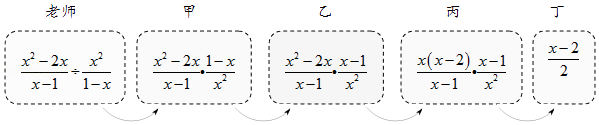
接力中，自己负责的一步出现错误的是（）

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

查看试题解析
3. 化简 $\frac{m - 1}{m} \div \frac{1 - m}{m^{2}}$ 是（）

A、m B、﹣m C、 D、-

查看试题解析
4. 下列变形正确的是（）.

A、 B、 C、 D、

查看试题解析
5. 下列关于分式的判断，正确的是（）

A、当x=2时， $\frac{x + 1}{x - 2}$ 的值为零 B、当x≠3时，有意义 C、无论x为何值，不可能得整数值 D、无论x为何值，的值总为正数

查看试题解析
6. 下列各式中，字母a不能取4的是（）

A、 B、 C、 D、

查看试题解析
7. 计算 $6 a^{3} b^{2} \cdot \frac{- 3 b}{2 a}$ 的结果为（）

A、3ab B、-3a²b² C、9a²b² D、-9a²b³

查看试题解析
8. 已知两个分式： $A ＝ \frac{4}{x^{2} － 4}$ ， $B ＝ \frac{1}{x ＋ 2} ＋ \frac{1}{2 － x}$ ，其中x≠±2，则A与B的关系是（）

A、相等 B、互为倒数 C、互为相反数 D、A大于B

查看试题解析
9. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为0，则x的值是（）

A、-1 B、1 C、±1 D、不存在

查看试题解析
10. 不改变分式的值，使分式 $\frac{\frac{1}{5} x - \frac{1}{10} y}{\frac{1}{3} x + \frac{1}{9} y}$ 的各项系数化为整数，分子、分母应乘以（）

A、10 B、9 C、45 D、90

查看试题解析

二、填空题

11. 已知 $\frac{1}{a} + \frac{1}{b} = 3$ ，求 $\frac{5 a + 7 a b + 5 b}{a - 6 a b + b}$ ＝．

查看试题解析
12. 不改变分式的值，将分式 $\frac{x + \frac{1}{3} y}{\frac{2}{5} x - \frac{1}{2} y}$ 的分子、分母的各项系数都化为整数．

查看试题解析
13. 已知 $\frac{3 x - 4}{(x - 1) (x - 2)}$ = $\frac{A}{x - 1}$ + $\frac{B}{x - 2}$ ，则实数A= ．

查看试题解析
14. 设m是方程x²﹣3x+1=0的一个实数根，则 $\frac{m^{4} + m^{2} + 1}{m^{2}}$ = ．

查看试题解析
15. 若 $\frac{1}{n (n + 1)} = \frac{a}{n} + \frac{b}{n + 1}$ ，对于任意正整数 $n$ 都成立，则 $a$ = ， $b$ = ；根据上面的式子，计算 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots \dots + \frac{1}{9 \times 10}$ = .

查看试题解析
16. 计算： $\frac{4}{a^{2} - 4} + \frac{2}{a + 2} - \frac{2}{a - 2}$ ．

查看试题解析

三、计算题

17. 计算

(1)、 $\frac{{ab}^{2}}{2 c^{2}} \div \frac{- 3 a^{2} b^{2}}{4 cd}$

(2)、 $\frac{2}{x + 3} - \frac{1}{x^{2} - 9} \div \frac{x}{x^{2} - 6 x + 9}$

查看试题解析
18.

(1)、计算： ${(\frac{1}{2})}^{- 1}$ －(2015－ $\sqrt{3}$ )⁰― $| \begin{matrix} 2 \end{matrix} |$ ；

(2)、化简： $\frac{a^{2} - 2 a + 1}{a - 1}$ －(a－2).

查看试题解析

四、解答题

19. 先化简，再求值：[1＋ $\frac{2 x- 4}{（ x+ 1 ）（ x- 2 ）}$ ]÷ $\frac{x+ 3}{x^{2} - 1}$ ，其中x＝6．

查看试题解析
20.
先化简，再求值： $(\frac{3}{x - 1} - x - 1) \div \frac{x - 2}{x^{2} - 2 x + 1}$ ，其中x是不等式组的一个整数解．

查看试题解析
21. 已知 $T = \frac{a^{2} - 9}{a {(a + 3)}^{2}} + \frac{6}{a (a + 3)}$

(1)、化简T。

(2)、若正方形ABCD的边长为a，且它的面积为9，求T的值。

查看试题解析
22. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = 2$ 且 $b + d + f \neq 0$ .

(1)、求 $\frac{a + c + e}{b + d + f}$ 的值；

(2)、若 $a - 2 c + 3 e = 5$ ，求 $b - 2 d + 3 f$ 的值.

查看试题解析
23. 已知分式M= $\frac{x}{x - 3}$ + $\frac{y}{y - 3}$ ．

(1)、若x=6，y=6，求M的值；

(2)、若x+y=3，xy=2，求M的值？

查看试题解析
24. 我们知道：分式和分数有着很多的相似点．如类比分数的基本性质，我们得到了分式的基本性质；类比分数的运算法则，我们得到了分式的运算法则，等等．小学里，把分子比分母小的分数叫做真分数．类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式．对于任何一个假分式都可以化成整式与真分式的和的形式，
如： $\frac{x + 1}{x - 1}$ = $\frac{x - 1 + 2}{x - 1}$ = $\frac{x - 1}{x - 1}$ + $\frac{2}{x - 1}$ =1+ $\frac{2}{x - 1}$ ；
$\frac{2 x - 3}{x + 1}$ = $\frac{2 x + 2 - 5}{x + 1}$ = $\frac{2 x + 2}{x + 1}$ + $\frac{- 5}{x + 1}$ =2+（﹣ $\frac{5}{x - 1}$ ）．

(1)、下列分式中，属于真分式的是：（填序号）；
① $\frac{a - 2}{a + 1}$
② $\frac{x^{2}}{x + 1}$
③ $\frac{2 b}{b^{2} + 3}$
④ $\frac{a^{2} + 3}{a^{2} - 1}$

(2)、将假分式 $\frac{4 a + 3}{2 a - 1}$ 化成整式与真分式的和的形式为： $\frac{4 a + 3}{2 a - 1}$ =+ ，若假分式 $\frac{4 a + 3}{2 a - 1}$ 的值为正整数，则整数a的值为；

(3)、将假分式 $\frac{a^{2} + 3}{a - 1}$ 化成整式与真分式的和的形式： $\frac{a^{2} + 3}{a - 1}$ = ．

查看试题解析