2018-2019学年初中数学浙教版八年级下册4.2 平行四边形 同步练习
试卷更新日期：2019-02-27 类型：同步测试
一、单选题
-
1. 平行四边形相邻两角中，其中一个角的度数y与另一个角的度数x 之间的关系是（ ）A、y=x B、y=90–x C、y=180–x D、y=180+x2. 如图，将▱ABCD折叠，使顶点D恰好落在AB边上的点M处，折痕为AN，那么对于结论：①MN∥BC；②MN＝AM.下列说法正确的是（ ）
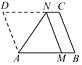A、①②都对 B、①②都错 C、①对，②错 D、①错，②对3. 如图所示，在平面直角坐标系内，原点O恰好是▱ABCD对角线的交点．若A点坐标为(2，3)，则C点坐标为（ ）
A、(－3，－2) B、(－2，3) C、(－2，－3) D、(2，－3)4. 在▱ABCD中，对角线AC，BD相交于点O，AC=8，BD=10，那么BC的取值范围是（ ）A、8<BC<10 B、2<BC<18 C、1<BC<8 D、1<BC<95. 平行四边形的一条边长是10cm，那么它的两条对角线的长可能是（ ）A、6cm和8cm B、10cm和20cm C、8cm和12cm D、12cm和32cm6. 平行四边形ABCD 中，有两个内角的比为1：2，则这个平行四边形中较小的内角是（ ）A、45° B、60° C、90° D、120°7. 如图，AB∥EF，C是EF上一个动点，当点C的位置变化时，△ABC的面积将（ ）
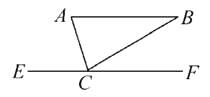A、变大 B、变小 C、不变 D、变大变小要看点C向左还是向右移动8. 如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，点D在BC上，以AC为对角线的所有▱ADCE中，DE最小的值是（ ）
A、2 B、3 C、4 D、59. 如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（ ）①∠DCF= ∠BCD；②EF=CF；③∠DFE=3∠AEF；④S△BEC=2S△CEF ．
A、①②③ B、②③④ C、①②④ D、①③④10. 如图，△ABC的面积为16，点D是BC边上一点，且BD＝ BC，点G是AB边上一点，点H在△ABC内部，BD∥GH，且BD＝GH.则图中阴影部分的面积是（ ）
A、3 B、4 C、5 D、6二、填空题
-
11. 如图，在▱ABCD中，∠A=70°，DC=DB，则∠CDB= ．
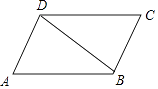12. 如图，平行四边形 中， 、 相交于点 ，若 ， ，则 的周长为.
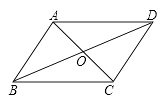13. 点O是平行四边形ABCD的对称中心，AD＞AB，E、F分别是AB边上的点，且EF＝ AB；G、H分别是BC边上的点，且GH＝ BC；若S1 ， S2分别表示∆EOF和∆GOH的面积，则S1 ， S2之间的等量关系是
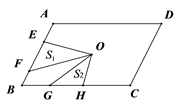14. 如图，在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE＝3.若平行四边形ABCD的周长是16，则EC的长为 ．
15. 如图，梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有对．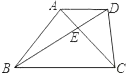
16. 如图，在周长为20cm的▱ABCD中，AB≠AD，AC，BD相交于点O，OE⊥BD交AD于E，则△ABE的周长为cm．
17. 如图，在 ABCD中，E、F分别是AB、DC边上的点，AF与DE相交于点P，BF与CE相交于点Q，若S△APD=16cm2 ， S△BQC=25cm2 ， 则图中阴影部分的面积为cm2 ．
三、解答题
-
18. 已知：如图，▱ABCD的对角线AC、BD相交于点O，过点O的直线分别与AD、BC相交于点E、F，求证：AE＝CF．
19. 在▱ABCD中，E是BC边上一点，F为DE上一点，若∠B=∠AFE，AB=AF．求证：△ADF≌△DEC．
20. 如图，把▱ABCD分成4个小平行四边形，已知▱AEOG，▱BFOG，▱CFOH的面积分别为8，10，30，求▱OEDH的面积．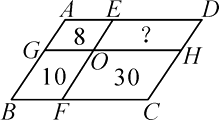
21. 如图，已知AD∥BC，AB∥EF，CD∥EG，且点E和点F，H，G分别在直线AD，BC上，EH平分∠FEG，∠A=∠D∠110°，线段EH的长是否是两条平行线AD，BC之间的距离？为什么？
22. 如图所示，直线L1∥L2 ， C1 ， C2 ， C3是L1上的三点，连接C1A，C1B，C2A，C2B，C3A，C3B，得△C1AB，△C2AB，△C3AB，试说明△C1AB，△C2AB，△C3AB的面积相等．
23. 如图，在△ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以2cm/s的速度运动，当点E先出发1s后，点F也从点B出发沿射线BC以 cm/s的速度运动，分别连结AF，CE．设点F运动时间为t（s），其中t＞0．
(1)、当t为何值时，∠BAF＜∠BAC；(2)、当t为何值时，AE=CF；(3)、当t为何值时，S△ABF+S△ACE＜S△ABC ．