2018-2019学年初中数学浙教版八年级下册4.1 多边形 同步练习
试卷更新日期：2019-02-27 类型：同步测试
一、单选题
-
1. 从一个七边形的某个顶点出发，分别连接这个点与其余各顶点，可以把一个七边形分割成（ ）个三角形．A、6 B、5 C、8 D、72. 四边形的四个内角（ ）A、可以都是锐角 B、可以都是钝角 C、可以都是直角 D、必须有两个锐角3. 小明在计算一个多边形的内角和时，漏掉了一个内角，结果得 1000°，则这个多边形是（ ）A、六边形 B、七边形 C、八边形 D、十边形4. 设四边形的内角和等于 ，五边形的外角和等于 ，则 与 的关系是（ ）A、
B、
C、
D、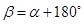
5. 把一张长方形纸片剪去其中某一个角，剩下的部分是一个多边形，则这个多边形的内角和不可能是（ ）
A、720° B、540° C、360° D、180°6. 一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（ ）A、8 B、7或8 C、6或7或8 D、7或8或97. 从五边形的一个顶点出发的对角线，把这个五边形分成（ ）个三角形.A、5 B、4 C、3 D、28. 在四边形ABCD中，∠A，∠B，∠C，∠D度数之比为1：2：3：3，则∠B的度数为（ ）
A、30° B、40° C、80° D、120°9. 如图，将一张四边形纸片沿直线剪开，如果剪开后的两个图形的内角和相等，下列四种剪法中，符合要求的是（ ）
A、①② B、①③ C、②④ D、③④10. 一个多边形最少可分割成五个三角形，则它是（ ）边形A、8 B、7 C、6 D、5二、填空题
-
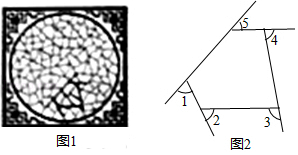
11. 若多边形的每一个內角均为135°，则这个多边形的边数为.12. 图1是我国古代建筑中的一种窗格，其中冰裂纹图案象征着坚冰出现裂纹并开始消溶，形状无一定规则，代表一种自然和谐美．图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形，则∠1+∠2+∠3+∠4+∠5=度．
13. 若正 边形的每个内角都等于150°，则 的值为 ．14. 如图，∠1，∠2，∠3，∠4是五边形ABCDE的4个外角．若∠A＝120°，则∠1＋∠2＋∠3＋∠4＝ ．
15. 一个八边形的所有内角都相等，它的每一个外角等于度．16. 如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于 ．
三、解答题
-
17. 一个多边形，它的内角和比外角和还多 180°，求这个多边形的边数.18. 一个多边形的内角和比它的外角的和的2倍还大180°，求这个多边形的边数．
19. 已知四边形的一个内角是56°，第二个内角是它的2倍，第三个内角比第二个内角小10°．求第四个内角的大小．20. 计算10边形的内角和及外角和．21. 如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O．
(1)、求证：BD=CE；(2)、若∠A=80°，求∠BOC的度数．22. 如图
(1)、内角和为2013°，小明为什么说不可能？
(2)、小华求的是几边形的内角和？
(3)、错把外角当内角的那个外角的度数你能求出吗？是多少度呢？23. 如图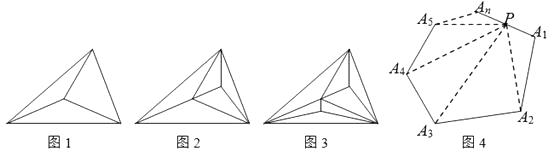
(1)、如图，在图1中，互不重叠的三角形共有3个，在图2中，互不重叠的三角形共有5个，在图3中，互不重叠的三角形共有7个，……，则在第n个图形中，互不重叠的三角形共有＿＿＿个.（用含n的代数式表示）
(2)、若在如图4所示的n边形中，P是A1An边上的点，分别连接PA2 ， PA3 ， PA4 ， …，PAn-1 ， 得到n－1个互不重叠的三角形.请根据这样的划分方法写出n边形的内角和公式.
(3)、反之，若在四边形内部有n个不同的点，按照（1）中的方法可得k个互不重叠的三角形，试探究n与k的关系24. 探究归纳题：
(1)、试验分析：如图1，经过A点可以做条对角线；同样，经过B点可以做条；经过C点可以做条；经过D点可以做条对角线.
通过以上分析和总结，图1共有条对角线.
(2)、拓展延伸：运用（1）的分析方法，可得：
图2共有条对角线；
图3共有条对角线；
(3)、探索归纳：对于n边形(n>3)，共有条对角线．(用含n的式子表示)
(4)、特例验证：十边形有对角线.