2018-2019学年初中数学浙教版八年级下册3.3 方差和标准差 同步练习

试卷更新日期：2019-02-27 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 某校九年级举办传统文化进校园朗诵大赛，小明同学根据比赛中九位评委所给的某位参赛选手的分数，制作了一个表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（   ）

    中位数

    众数

    平均数

    方差

    9.2

    9.3

    9.1

    0.3

    A、中位数 B、众数 C、平均数 D、方差

    查看试题解析

  • 2. 如果一组数据6、7、x、9、5的平均数是2x，那么这组数据的方差为（   ）
    A、4 B、3 C、2 D、1

    查看试题解析

  • 3. 某排球队 6 名场上队员的身高（单位： cm ）是： 180 ， 184 ， 188 ， 190 ， 192 ， 194 .现用一名身高为 186 cm 的队员换下场上身高为 192 cm 的队员，与换人前相比，场上队员的身高（    ）
    A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

    查看试题解析

  • 4. 已知一组数据：92，94，98，91，95的中位数为a，方差为b，则a+b=（   ）
    A、98 B、99 C、100 D、102

    查看试题解析

  • 5. 若一组数据2、4、6、8、x的方差比另一组数据5、7、9、11、13的方差大，则 x 的值可以是（     ）
    A、12 B、10 C、2 D、0

    查看试题解析

  • 6. 为迎接中考体育加试，小刚和小亮分别统计了自己最近10次跳绳比赛，下列统计量中能用来比较两人成绩稳定程度的是（     ）
    A、平均数 B、中位数 C、众数 D、方差

    查看试题解析

  • 7. 一组数据：3，4，5，x，8 的众数是 5，则这组数据的方差是（   ）
    A、2 B、2.4 C、2.8 D、3

    查看试题解析

  • 8. 甲、乙、丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数 x¯ 与方差 s2 如下表：

    甲

    乙

    丙

    丁

    平均数 x¯ （米）

    11.1

    11.1

    10.9

    10.9

    方差 s2

    1.1

    1.2

    1.3

    1.4

    若要选一名成绩好且发挥稳定的同学参加比赛，则应该选择（   ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 9. 为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲，乙两组数据，如下表：

    甲

    2

    6

    7

    7

    8

    乙

    2

    3

    4

    8

    8

    类于以上数据，说法正确的是（     ）

    A、甲、乙的众数相同 B、甲、乙的中位数相同 C、甲的平均数小于乙的平均数 D、甲的方差小于乙的方差

    查看试题解析

  • 10. 以下说法中，①如果一组数据的标准差等于零，则这组中的每个数据都相等；②分别用一组数据中的每一个数减去平均数，再将所得的差相加．若和为零，则标准差为零；③在一组数据中去掉一个等于平均数的数，这组数据的平均数不变；④在一组数据中去掉一个等于平均数的数，这组数据的标准差不变，其中正确的有（   ）
    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 11. 甲、乙两名运动员进行了5次百米赛跑测试，两人的平均成绩都是13.3秒，而S甲2=3.7，S乙2=6.25，则两人中成绩较稳定的是 ．

    查看试题解析

  • 12. 实数x，y满足|x﹣y|=7，则实数x，y的方差为 ．

    查看试题解析

  • 13. 已知一组数据为：12，9，10，8，1l，则这组数据的方差是.

    查看试题解析

  • 14. 小明等五位同学以各自的年龄为一组数据，计算出这组数据的方差是0.5，则10年后小明等五位同学年龄的方差（填“不变”“增大”或“减小”）．

    查看试题解析

  • 15. 为了比较甲、乙两种水稻秧苗哪种出苗更整齐，各随机抽取50株，量出每株长度，发现两组秧苗的平均长度一样，甲、乙的方差分别是3.5，10.9，则出苗更整齐的是（填“甲”或“乙”）．

    查看试题解析

  • 16. 已知甲、乙两组数据的折线图如图，设甲、乙两组数据的方差分别为S甲2、S乙2 ， 则S甲2S乙2（填“＞”、“=”、“＜”）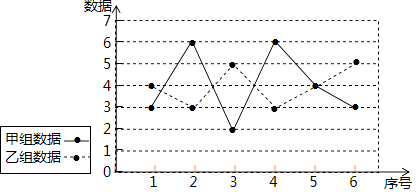

    查看试题解析

三、解答题

  • 17. 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：

    根据以上信息，整理分析数据如下：

    (1)、写出表格中a，b，c的值；
    (2)、分别运用上表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？

    查看试题解析

  • 18. 甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查，统计结果如下：（单位：年）

    甲厂：3，4，5，6，7  乙厂：4，4，5，6，6

    (1)、分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差；
    (2)、如果你是顾客，你会选购哪家电子厂的产品？说明理由.

    查看试题解析

  • 19. 某公司共25名员工，下表是他们月收入的资料．

    月收入/元

    45000

    18000

    10000

    5500

    4800

    3400

    3000

    2200

    人数

    1

    1

    1

    3

    6

    1

    11

    1

    (1)、该公司员工月收入的中位数是元，众数是元．
    (2)、根据上表，可以算得该公司员工月收入的平均数为6276元，你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由．

    查看试题解析

  • 20. 甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）： 

    甲：98，100，100，90，96，91，89，99，100，100，93

    乙：98，99，96，94，95，92，92，98，96，99，97

    (1)、他们的平均成绩分别是多少？
    (2)、甲、乙的11次单元测验成绩的标准差分别是多少？
    (3)、这两位同学的成绩各有什么特点？
    (4)、现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？

    查看试题解析

  • 21. 某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：

    (1)、请根据上表中的数据完成下表（注：方差的计算结果精确到0.1）
    (2)、根据综合评价得分统计表中的数据，请在下图中画出乙组综合评价得分的折线统计图．
    (3)、根据折线统计图中的信息，请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．

    查看试题解析