2017年吉林省吉林市高考数学三模试卷（理科）

试卷更新日期：2017-04-20 类型：高考模拟

进入出卷网下载

一、选择题

1. 设全集U=R，集合A={x|x＞1}，集合B={x|x＞p}，若（∁_UA）∩B=∅，则p应该满足的条件是（）

A、p＞1 B、p≥1 C、p＜1 D、p≤1

查看试题解析
2. 已知复数z= $\frac{i}{1 + i}$ ，其中i为虚数单位，则|z|=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
3. 已知向量 $\vec{a}$ =（x，2）， $\vec{b}$ =（2，1）， $\vec{c}$ =（3，x），若 $\vec{a}$ ∥ $\vec{b}$ ，则 $\vec{a}$ • $\vec{c}$ =（）

A、4 B、8 C、12 D、20

查看试题解析
4. 已知点F（2，0）是双曲线3x²﹣my²=3m（m＞0）的一个焦点，则此双曲线的离心率为（）

A、 $\frac{1}{2}$ B、 $\sqrt{3}$ C、2 D、4

查看试题解析
5. ${(\sqrt{x} + \frac{3}{x})}^{n}$ 的展开式中，各项系数之和为A，各项的二项式系数之和为B，若 $\frac{A}{B}$ =32，则n=（）

A、5 B、6 C、7 D、8

查看试题解析
6. 给出下列几个命题：

①命题p：任意x∈R，都有cosx≤1，则￢p：存在x₀∈R，使得cosx₀≤1
②命题“若a＞2且b＞2，则a+b＞4且ab＞4”的逆命题为假命题
③空间任意一点O和三点A，B，C，则 $\vec{O A}$ =3 $\vec{O B}$ =2 $\vec{O C}$ 是A，B，C三点共线的充分不必要条件
④线性回归方程y=bx+a对应的直线一定经过其样本数据点（x₁ ， y₁），（x₂ ， y₂），…，（x_n ， y_n）中的一个
其中不正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 若直角坐标平面内的两点P，Q满足条件：①P，Q都在函数y=f（x）的图象上；②P，Q关于原点对称，则称点对（P，Q）是函数y=f（x）的一对“友好点对”（点对（P，Q）与（Q，P）看作同一对“友好点对”）．已知函数f（x）= ${\begin{matrix} {(\frac{1}{2})}^{x} ， x > 0 \\ x + 1 ， x \leq 0 \end{matrix}$ ，则此函数的“友好点对”有（）

A、3对 B、2对 C、1对 D、0对

查看试题解析
8. 2002年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图）．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么sin2θ的值为（）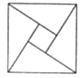

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{23}{24}$ D、 $\frac{24}{25}$

查看试题解析
9. 阅读程序框图，运行相应的程序，则输出i的值为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 中国有个名句“运筹帷幄之中，决胜千里之外．”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式（如下图所示），表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推．例如6613用算筹表示就是，则9117用算筹可表示为（）

A、 B、 C、 D、

查看试题解析
11. 已知数列{a_n}的各项均为正整数，其前n项和为S_n ， a_n₊₁= ${\begin{matrix} \frac{a_{n} + 1}{2} ， a_{n} 是奇数 \\ 3 a_{n} - 1 ， a_{n} 是偶数 \end{matrix}$ ，若S₃=10，则S₁₈₀=（）

A、600或900 B、900或560 C、900 D、600

查看试题解析
12. 定义在区间D上的函数f（x）和g（x），如果对任意x∈D，都有|f（x）﹣g（x）|≤1成立，则称f（x）在区间D上可被g（x）替代，D称为“替代区间”．给出以下问题：

①f（x）=x²+1在区间（﹣∞，+∞）上可被g（x）=x²+ $\frac{1}{2}$ 替代；
②如果f（x）=lnx在区间[1，e]可被g（x）=x﹣b替代，则﹣2≤b≤2；
③设f（x）=lg（ax²+x）（x∈D₁），g（x）=sinx（x∈D₁），则存在实数a（a≠0）及区间D₁ ， D₂ ，使得f（x）在区间D₁∩D₂上被g（x）替代．
其中真命题是（）

A、①②③ B、②③ C、① D、①②

查看试题解析

二、填空题

13. 设x，y满足不等式组 ${\begin{matrix} x + y - 6 \leq 0 \\ x - y - 2 \leq 0 \\ x \geq 0 \end{matrix}$ ，则z=﹣2x+y的最小值为

查看试题解析
14. 已知等差数列{a_n}中，a₅+a₇= $\int_{0}^{π} \sin x d x$ ，则a₄+a₆+a₈=

查看试题解析
15.
某几何体的三视图如图所示，且该几何体的体积为2，则正视图的面积=

查看试题解析
16. 已知A，B是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1和双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1的公共顶点，其中a＞b＞0，P是双曲线上的动点，M是椭圆上的动点（P，M都异于A，B），且满足 $\vec{P A} + \vec{P B}$ =λ（ $\vec{M A} + \vec{M B}$ ）（λ∈R），设直线AP，BP，AM，BM的斜率分别为k₁ ， k₂ ， k₃ ， k₄ ，若k₁+k₂= $\sqrt{3}$ ，则k₃+k₄= ．

查看试题解析

三、解答题

17. 已知函数f（x）=cos2x+2sin²x+2sinx．

（Ⅰ）将函数f（2x）的图象向右平移 $\frac{π}{6}$ 个单位得到函数g（x）的图象，若x∈[ $\frac{π}{12}$ ， $\frac{π}{12}$ ]，求函数g（x）的值域；
（Ⅱ）已知a，b，c分别为△ABC中角A，B，C的对边，且满足f（A）= $\sqrt{3}$ +1，A∈（0， $\frac{π}{2}$ ），a=2 $\sqrt{3}$ ，b=2，求△ABC的面积．

查看试题解析
18. 据《中国新闻网》10月21日报道，全国很多省市将英语考试作为高考改革的重点，一时间“英语考试该如何改”引起广泛关注．为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人调查，就是否“取消英语听力”的问题，调查统计的结果如下表：
态度
调查人群
应该取消
应该保留
无所谓
在校学生
2100人
120人
y人
社会人士
600人
x人
z人
已知在全体样本中随机抽取1人，抽到持“应该保留”态度的人的概率为0.05．
（Ⅰ）现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（Ⅱ）在持“应该保留”态度的人中，用分层抽样的方法抽取6人平均分成两组进行深入交流，求第一组中在校学生人数ξ的分布列和数学期望．

查看试题解析
19.
已知四棱锥P﹣ABCD中，底面为矩形，PA⊥底面ABCD，PA=BC=1，AB=2，M为PC中点．

（Ⅰ）在图中作出平面ADM与PB的交点N，并指出点N所在位置（不要求给出理由）；
（Ⅱ）在线段CD上是否存在一点E，使得直线AE与平面ADM所成角的正弦值为 $\frac{\sqrt{10}}{10}$ ，若存在，请说明点E的位置；若不存在，请说明理由；
（Ⅲ）求二面角A﹣MD﹣C的余弦值．

查看试题解析
20. 已知O为坐标原点，抛物线C：y²=nx（n＞0）在第一象限内的点P（2，t）到焦点的距离为 $\frac{5}{2}$ ，曲线C在点P处的切线交x轴于点Q，直线l₁经过点Q且垂直于x轴．

（Ⅰ）求线段OQ的长；
（Ⅱ）设不经过点P和Q的动直线l₂：x=my+b交曲线C于点A和B，交l₁于点E，若直线PA，PE，PB的斜率依次成等差数列，试问：l₂是否过定点？请说明理由．

查看试题解析
21. 已知函数f（x）=x²﹣（a+2）x+alnx，其中常数a＞0．

（Ⅰ）当a＞2时，求函数f（x）的单调递增区间；
（Ⅱ）设定义在D上的函数y=h（x）在点P（x₀ ， h（x₀））处的切线方程为l：y=g（x），若 $\frac{h (x) - g (x)}{x - x_{0}}$ ＞0在D内恒成立，则称P为函数y=h（x）的“类对称点”．当a=4时，试问y=f（x）是否存在“类对称点”，若存在，请至少求出一个“类对称点”的横坐标；若不存在，请说明理由．

查看试题解析
22. 选修4-4：坐标系与参数方程
以直角坐标系xOy的原点为极点，x轴的非负半轴为极轴建立极坐标系，且两坐标系相同的长度单位．已知点N的极坐标为（ $\sqrt{2}$ ， $\frac{π}{4}$ ），M是曲线C₁：ρ=1上任意一点，点G满足 $\vec{O G} = \vec{O M} + \vec{O N}$ ，设点G的轨迹为曲线C₂ ．

(1)、求曲线C₂的直角坐标方程；

(2)、若过点P（2，0）的直线l的参数方程为 ${\begin{matrix} x = 2 - \frac{1}{2} t \\ y = \frac{\sqrt{3}}{2} t \end{matrix}$ （t为参数），且直线l与曲线C₂交于A，B两点，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的值．

查看试题解析
23. 选修4-5：不等式选讲
已知定义在R上的函数f（x）=|x﹣m|+|x|，m∈N^* ，存在实数x使f（x）＜2成立．
（Ⅰ）求实数m的值；
（Ⅱ）若α，β＞1，f（α）+f（β）=2，求证： $\frac{4}{α}$ + $\frac{1}{β}$ ≥ $\frac{9}{2}$ ．

查看试题解析