四川省宜宾市叙州区2018-2019学年理数高三上学期期末考试试卷
试卷更新日期:2019-02-27 类型:期末考试
一、单选题
-
1. 设全集 ,集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知复数 满足 ,则 ( )A、
2. 已知复数 满足 ,则 ( )A、 B、
B、 C、
C、 D、
D、 3. 在 中, , ,那么 等于( )A、 B、 C、 或
3. 在 中, , ,那么 等于( )A、 B、 C、 或 D、 或
D、 或 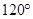 4. 已知随机变量v服从正态分布 则 ( )A、0.89 B、0.78 C、0.22 D、0.115. 已知向量 , ,若 ,则 与 的夹角为( )A、
4. 已知随机变量v服从正态分布 则 ( )A、0.89 B、0.78 C、0.22 D、0.115. 已知向量 , ,若 ,则 与 的夹角为( )A、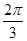 B、
B、 C、
D、
6. 设等差数列{an}的前n项和为Sn , 若Sm-1=-2,Sm=0,Sm+1=3,则m=( )A、3 B、4 C、5 D、67. 如图所示是一个几何体的三视图,则这个几何体外接球的表面积为
C、
D、
6. 设等差数列{an}的前n项和为Sn , 若Sm-1=-2,Sm=0,Sm+1=3,则m=( )A、3 B、4 C、5 D、67. 如图所示是一个几何体的三视图,则这个几何体外接球的表面积为 A、
A、 B、
B、 C、
C、 D、
D、 8. 我国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则此人第一天走的路程为( )A、192里 B、96里 C、63里 D、6里9. 函数 在区间 , 内是增函数, 则实数 的取值范围是A、
8. 我国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则此人第一天走的路程为( )A、192里 B、96里 C、63里 D、6里9. 函数 在区间 , 内是增函数, 则实数 的取值范围是A、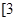 ,
,  B、
B、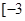 ,
,  C、
C、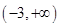 D、
D、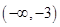 10. 已知抛物线 的准线过双曲线 的左焦点且与双曲线交于 、 两点, 为坐标原点,且 的面积为 ,则双曲线的离心率为A、 B、4 C、3 D、211. 已知函数 , , 为 的零点, 为 图象的对称轴, 且 在 , 上单调, 则 的最大值为A、11 B、9 C、7 D、512. 如图所示的程序框图,输出的 的值为
10. 已知抛物线 的准线过双曲线 的左焦点且与双曲线交于 、 两点, 为坐标原点,且 的面积为 ,则双曲线的离心率为A、 B、4 C、3 D、211. 已知函数 , , 为 的零点, 为 图象的对称轴, 且 在 , 上单调, 则 的最大值为A、11 B、9 C、7 D、512. 如图所示的程序框图,输出的 的值为 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
13. 已知 关于 的展开式中,只有第4项的二项式系数最大,则展开式的系数之和为.14. 已知实数 , 满足不等式组 则 的最小值为 .15. AB为过抛物线 焦点F的一条弦,设 , ,以下结论正确的是 ,
,且 的最小值为4 以AF为直径的圆与x轴相切.
16. 当 , 时,不等式 恒成立,则实数 的取值范围是 .三、解答题
-
17. 在 中,内角 , , 的对边分别为 , , ,已知 , ,且 .(1)、求角 的大小;(2)、若 , ,求 的面积.18. 2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在 内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

表1:设备改造后样本的频数分布表
 (1)、完成下面的 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
(1)、完成下面的 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关; (2)、根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;(3)、企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在 内的定为一等品,每件售价240元;质量指标值落在 或 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为 (单位:元),求 的分布列和数学期望.
(2)、根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;(3)、企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在 内的定为一等品,每件售价240元;质量指标值落在 或 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为 (单位:元),求 的分布列和数学期望.附:
0.150
0.100
0.050
0.025
0.010
2.072
2.706
3.841
5.024
6.635
19. 如图,在直三棱柱 侧棱和底面垂直的棱柱 中,平面 侧面 , ,线段AC、 上分别有一点E、F且满足 , .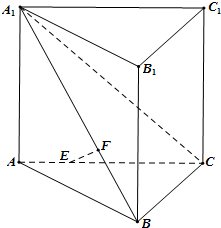 (1)、求证: ;(2)、求点E到直线 的距离;(3)、求二面角 的平面角的余弦值.20. 抛物线 的焦点为 ,过点 的直线交抛物线于 , 两点.(1)、 为坐标原点,求证: ;(2)、设点 在线段 上运动,原点 关于点 的对称点为 ,求四边形 面积的最小值21. 定义在 上的函数 满足 , .(1)、求函数 的解析式;(2)、求函数 的单调区间;(3)、如果 、 、 满足 ,那么称 比 更靠近 .当 且 时,试比较 和 哪个更靠近 ,并说明理由.
(1)、求证: ;(2)、求点E到直线 的距离;(3)、求二面角 的平面角的余弦值.20. 抛物线 的焦点为 ,过点 的直线交抛物线于 , 两点.(1)、 为坐标原点,求证: ;(2)、设点 在线段 上运动,原点 关于点 的对称点为 ,求四边形 面积的最小值21. 定义在 上的函数 满足 , .(1)、求函数 的解析式;(2)、求函数 的单调区间;(3)、如果 、 、 满足 ,那么称 比 更靠近 .当 且 时,试比较 和 哪个更靠近 ,并说明理由.
