2017年湖南省郴州市高考数学二模试卷（理科）

试卷更新日期：2017-04-20 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知x，y∈R，i是虚数单位．若x+yi与 $\frac{3 + i}{1 + i}$ 互为共轭复数，则x+y=（）

A、0 B、1 C、2 D、3

查看试题解析
2. 已知 $\vec{a} ， \vec{b}$ 均为单位向量，且 $(2 \vec{a} + \vec{b}) \cdot (\vec{a} - 2 \vec{b}) = - \frac{3 \sqrt{3}}{2}$ ，则向量 $\vec{a} ， \vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{3 π}{4}$ D、 $\frac{5 π}{6}$

查看试题解析
3. 已知 $α \in (0 ， \frac{π}{6})$ ， $\sin (α + \frac{π}{3}) = \frac{12}{13}$ ，则 $\cos (\frac{π}{6} - α)$ =（）

A、 $\frac{5}{12}$ B、 $\frac{12}{13}$ C、 $- \frac{5}{13}$ D、 $- \frac{12}{13}$

查看试题解析
4. 我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水．天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸．若盆中积水深九寸，则平地降雨量是（）

（注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸；③台体的体积公式V= $\frac{1}{3} (S_{上} + \sqrt{S_{上} S_{下}} + S_{下}) \cdot h$

A、2寸 B、3寸 C、4寸 D、5寸

查看试题解析
5. 考拉兹猜想又名3n+1猜想，是指对于每一个正整数，如果它是奇数，则对它乘3再加1；如果它是偶数，则对它除以2．如此循环，最终都能得到1．阅读如图所示的程序框图，运行相应程序，输出的结果i=（）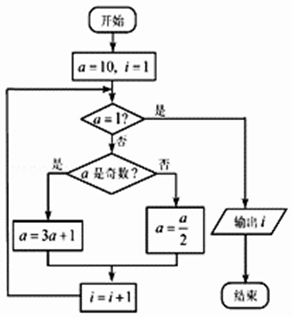

A、4 B、5 C、6 D、7

查看试题解析
6. 已知某三棱锥的三视图如图所示，正视图和俯视图都是等腰直角三角形，则该三棱锥中最长的棱长为（）

A、 $2 \sqrt{3}$ B、 $2 \sqrt{2}$ C、 $\sqrt{5}$ D、2

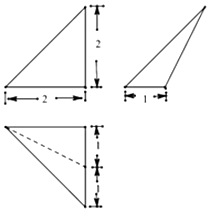查看试题解析
7. 已知函数f（x）是奇函数，当x＞0时，f（x）=a^x（x＞0且a≠1），且f（log $_{\frac{1}{2}}$ 4）=﹣3，则a的值为（）

A、 $\sqrt{3}$ B、3 C、9 D、 $\frac{3}{2}$

查看试题解析
8. 设关于x，y的不等式组 ${\begin{matrix} 2 x - y + 1 > 0 \\ x + m < 0 \\ y - m > 0 \end{matrix}$ 表示的平面区域内存在点P（x₀ ， y₀），满足x₀﹣2y₀=2，求得m的取值范围是（）

A、 $(- \infty ， \frac{4}{3})$ B、 $(- \infty ， \frac{1}{3})$ C、 $(- \infty ， - \frac{2}{3})$ D、 $(- \infty ， - \frac{5}{3})$

查看试题解析
9. 将边长为 $\sqrt{2}$ 的正方形ABCD沿对角线AC折成一个直二面角B﹣AC﹣D．则四面体ABCD的内切球的半径为（）

A、1 B、 $2 \sqrt{2} - \sqrt{3}$ C、 $\sqrt{2}$ -1 D、 $2 - \sqrt{3}$

查看试题解析
10. 已知F为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ 1（a＞0，b＞0）的右焦点，定点A为双曲线虚轴的一个顶点，过F，A的直线与双曲线的一条渐近线在y轴左侧的交点为B，若 $\vec{F A}$ =（ $\sqrt{2}$ ﹣1） $\vec{A B}$ ，则此双曲线的离心率是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 $\sqrt{2}$ D、 $\sqrt{5}$

查看试题解析
11. 在△ABC中，A₁ ， B₁分别是边BA，CB的中点，A₂ ， B₂分别是线段A₁A，B₁B的中点，…，A_n ， B_n分别是线段 $A_{n - 1} A ， B_{n - 1} B (n \in N^{*} ， n > 1)$ 的中点，设数列{a_n}，{b_n}满足：向量 $\vec{B_{n} A_{n}} = a_{n} \vec{C A} + b_{n} \vec{C B} (n \in N^{*})$ ，有下列四个命题，其中假命题是（）

A、数列{a_n}是单调递增数列，数列{b_n}是单调递减数列 B、数列{a_n+b_n}是等比数列 C、数列 ${\frac{a_{n}}{b_{n}}}$ 有最小值，无最大值 D、若△ABC中，C=90°，CA=CB，则 $| \vec{B_{n} A_{n}} |$ 最小时， $a_{n} + b_{n} = \frac{1}{2}$

查看试题解析
12. 若方程|x²﹣2x﹣1|﹣t=0有四个不同的实数根x₁、x₂、x₃、x4，且x₁＜x₂＜x₃＜x₄ ，则2（x₄﹣x₁）+（x₃﹣x₂）的取值范围是（）

A、（8，6 $\sqrt{2}$ ） B、（6 $\sqrt{2}$ ，4 $\sqrt{5}$ ） C、[8，4 $\sqrt{5}$ ] D、（8，4 $\sqrt{5}$ ]

查看试题解析

二、填空题

13. 若命题p：“ $\exists x_{0} \in R ， 2^{x_{0}} - 2 \leq a^{2} - 3 a$ ”是假命题，则实数a的取值范围是．

查看试题解析
14. 两所学校分别有2名，3名学生获奖，这5名学生要排成一排合影，则存在同校学生排在一起的概率为.

查看试题解析
15. 过点 $M (\frac{1}{2} ， 1)$ 的直线l与圆C：（x﹣1）²+y²=4交于A、B两点，C为圆心，当∠ACB最小时，直线l的方程为．

查看试题解析
16. 已知函数f（x）=2|cosx|sinx+sin2x，给出下列四个命题：

①函数f（x）的图象关于直线 $x = \frac{π}{4}$ 对称；
②函数f（x）在区间 $[- \frac{π}{4}, \frac{π}{4}]$ 上单调递增；
③函数f（x）的最小正周期为π；
④函数f（x）的值域为[﹣2，2]．
其中真命题的序号是．（将你认为真命题的序号都填上）

查看试题解析

三、解答题

17. 已知等差数列{a_n}．满足：a_n₊₁＞a_n（n∈N^*），a₁=1，该数列的前三项分别加上1，1，3后成等比数列，a_n+2log₂b_n=﹣1．
（Ⅰ）分别求数列{a_n}，{b_n}的通项公式；
（Ⅱ）求数列{a_n•b_n}的前n项和T_n ．

查看试题解析
18. 在△ABC中，a，b，c分别是角A，B，C的对边，且2cosAcosC（tanAtanC﹣1）=1．
（Ⅰ）求B的大小；
（Ⅱ）若 $a + c = \frac{3 \sqrt{3}}{2}$ ， $b = \sqrt{3}$ ，求△ABC的面积．

查看试题解析
19. 如图，菱形ABCD中，∠ABC=60°，AC与BD相交于点O，AE⊥平面ABCD，CF∥AE，AB=2，CF=3．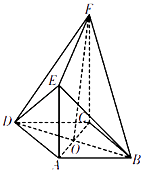

(1)、求证：BD⊥平面ACFE；

(2)、当直线FO与平面BED所成角的大小为45°时，求AE的长度．

查看试题解析
20. 某水泥厂销售工作人员根据以往该厂的销售情况，绘制了该厂日销售量的频率分布直方图，如图所示：将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．

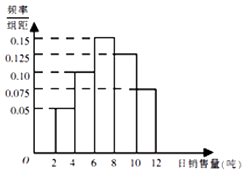(1)、求未来3天内，连续2天日销售量不低于8吨，另一天日销售量低于8吨的概率；

(2)、用X表示未来3天内日销售量不低于8吨的天数，求随机变量X的分布列及数学期望．

查看试题解析
21. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{1}{2}$ ，且过点 $(1, \frac{3}{2})$ ．若点M（x₀ ， y₀）在椭圆C上，则点 $N (\frac{x_{0}}{a}, \frac{y_{0}}{b})$ 称为点M的一个“椭点”．

(1)、求椭圆C的标准方程；

(2)、若直线l：y=kx+m与椭圆C相交于A，B两点，且A，B两点的“椭点”分别为P，Q，以PQ为直径的圆经过坐标原点，试求△AOB的面积．

查看试题解析
22. 已知函数f（x）=xlnx，g（x）=﹣x²+ax﹣3．

(1)、求函数f（x）在[t，t+2]（t＞0）上的最小值；

(2)、对一切x∈（0，+∞），2f（x）≥g（x）恒成立，求实数a的取值范围．

(3)、探讨函数F（x）=lnx﹣ $\frac{1}{e^{x}}$ + $\frac{2}{e x}$ 是否存在零点？若存在，求出函数F（x）的零点，若不存在，请说明理由．

查看试题解析