2018-2019学年初中数学浙教版七年级下册3.5 整式的化简同步练习

试卷更新日期：2019-02-27 类型：同步测试

进入出卷网下载

一、单选题

1. 如果多项式p=a²+2b²+2a+4b+2008，则p的最小值是（）

A、2005 B、2006 C、2007 D、2008

查看试题解析
2. 不论x取何值，x﹣x²﹣1的值都（）

A、大于等于﹣ $\frac{3}{4}$ B、小于等于﹣ $\frac{3}{4}$ C、有最小值﹣ $\frac{3}{4}$ D、恒大于零

查看试题解析
3. 若a²﹣b²= $\frac{1}{8}$ ，a+b= $\frac{1}{4}$ ，则a﹣b的值为（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
4. 已知a²+b²=6ab且a＞b＞0，则 $\frac{a + b}{a - b}$ 的值为（）

A、 $\sqrt{2}$ B、± $\sqrt{2}$ C、2 D、±2

查看试题解析
5. 若S=（1﹣ $\frac{1}{2^{2}}$ ）（1﹣ $\frac{1}{3^{2}}$ ）（1﹣ $\frac{1}{4^{2}}$ ）…（1﹣ $\frac{1}{2016^{2}}$ ），则S的值为（）

A、 $\frac{2013}{2016}$ B、 $\frac{2015}{2016}$ C、 $\frac{2015}{4032}$ D、 $\frac{2017}{4032}$

查看试题解析
6. 若1≤x≤4，则化简 $| 1 - x | - \sqrt{x^{2} - 8 x + 16}$ 的结果是（）

A、 $2 x - 5$ B、 $3$ C、 $3 - 2 x$ D、— $\frac{1}{x}$ 3

查看试题解析
7. 设x，y为实数，5x²+4y²﹣8xy+2x+4的最小值为（）

A、1 B、2 C、3 D、5

查看试题解析
8. 下列各式中，一定成立的是（）

A、 ${(x + y)}^{2} = x^{2} + y^{2}$ B、 $(x + 6) (x - 6) = x^{2} - 6$ C、 ${(x - y)}^{2} = {(y - x)}^{2}$ D、 $(3 x - y) (- 3 x + y) = 9 x^{2} - y^{2}$

查看试题解析
9. 若实数abc满足a²+b²+c²=9，代数式（a﹣b）²+（b﹣c）²+（c﹣a）²的最大值是（）

A、27 B、18 C、15 D、12

查看试题解析
10. 已知 $x + \frac{1}{x} = 3$ ，则下列三个等式：① $x^{2} + \frac{1}{x^{2}} = 7$ ，② $x - \frac{1}{x} = \sqrt{5}$ ，③ $2 x^{2} - 6 x = - 2$ 中，正确的个数有（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析

二、填空题

11. （-x+2y）（-x-2y）等于；

查看试题解析
12.

(1)、计算： $a^{2} \cdot a^{3}$ 的结果等于；

(2)、已知 $a + b = 3$ ， $a - b = 5$ ，则代数式 $a^{2} + b^{2}$ 的值是.

查看试题解析
13. 已知 $x + \frac{1}{x} = 5$ ，那么 $x^{2} + \frac{1}{x^{2}}$ =。

查看试题解析
14. (m+n+p+q) (m-n-p-q)＝（）²-（）² ．

查看试题解析
15. 一个四边形的边长依次为a，b，c，d，且a²+b²+c²+d²＝2ac+2bd，则这个四边形是。

查看试题解析
16. 计算： ${(x- \frac{1}{3})}^{2} {(x^{2} + \frac{1}{9})}^{2} {(x + \frac{1}{3})}^{2}$ =

查看试题解析
17. 计算：1.99²-1.98×1.99+0.99²=

查看试题解析

三、解答题

18. 先化简，再求值： $\frac{x - 2}{x^{2} - 1} \cdot \frac{x + 1}{x^{2} - 4 x + 4} + \frac{1}{x - 1}$ ，其中x是从-1、0、1、2中选取一个合适的数．

查看试题解析
19. 已知：x²﹣y²=12，x+y=3，求2x²﹣2xy的值．

查看试题解析
20. 先化简，再求值：[（x﹣2y）²﹣x（x﹣4y）﹣8xy]÷4y，其中x=﹣1，y=2．

查看试题解析
21. 如图1是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．

(1)、这个几何体模型的名称是．

(2)、如图2是根据a ， b ， h的取值画出的几何体的主视图和俯视图（图中实线表示的长方形），请在网格中画出该几何体的左视图．若h=a+b ，且a ， b满足 $\frac{1}{4}$ a²+b²﹣a﹣6b+10=0，求该几何体的表面积．

查看试题解析
22. 如果一个自然数能表示为两个自然数的平方差，那么称这个自然数为智慧数，例如：16=5²﹣3² ， 16就是一个智慧数，小明和小王对自然数中的智慧数进行了如下的探索：
小明的方法是一个一个找出来的：0=0²﹣0² ， 1=1²﹣0² ， 3=2²﹣1² ， 4=2²﹣0² ， 5=3²﹣2² ， 7=4²﹣3² ， 8=3²﹣1² ， 9=5²﹣4² ， 11=6²﹣5² ， …
小王认为小明的方法太麻烦，他想到：
设k是自然数，由于（k+1）²﹣k²=（k+1+k）（k+1﹣k）=2k+1．
所以，自然数中所有奇数都是智慧数．
问题：

(1)、根据上述方法，自然数中第12个智慧数是

(2)、他们发现0，4，8是智慧数，由此猜测4k（k≥3且k为正整数）都是智慧数，请你参考小王的办法证明4k（k≥3且k为正整数）都是智慧数．

(3)、他们还发现2，6，10都不是智慧数，由此猜测4k+2（k为自然数）都不是智慧数，请利用所学的知识判断26是否是智慧数，并说明理由．

查看试题解析
23. 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片边长为a的正方形，B种纸片是边长为b的正方形，C种纸片长为a、宽为b的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．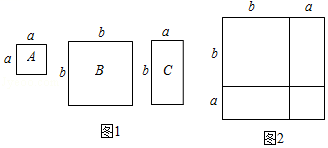

(1)、请用两种不同的方法求图2大正方形的面积．

(2)、观察图2，请你写出下列三个代数式：（a+b）² ， a²+b² ， ab之间的等量关系．

(3)、根据（2）题中的等量关系，解决如下问题：
①已知：a+b=5，a²+b²=11，求ab的值；
②已知（2018﹣a）²+（a﹣2017）²=5，求（2018﹣a）（a﹣2017）的值．

查看试题解析

2018-2019学年初中数学浙教版七年级下册3.5 整式的化简 同步练习

一、单选题

二、填空题

三、解答题

2018-2019学年初中数学浙教版七年级下册3.5 整式的化简同步练习