2018-2019学年初中数学浙教版七年级下册3.4 乘法公式 同步练习
试卷更新日期:2019-02-27 类型:同步测试
一、单选题
-
1. 下列运算正确的是( )A、3a2+2b3=5a2b3 B、(a+b)2=a2+b2 C、(-a-2b3)3=a6b9 D、1 - 4m + 4m2= (2m -1)2. 若x2﹣xy+2=0,y2﹣xy﹣4=0,则x﹣y的值是( )A、﹣2 B、2 C、±2 D、±3. 如果x2+6x+k2恰好是一个整式的平方,那么常数k的值为( )A、3 B、 C、
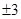 D、9
4. 下列算式能用平方差公式计算的是( )A、
D、9
4. 下列算式能用平方差公式计算的是( )A、 B、
B、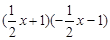 C、
C、 D、
D、 5. 要使 成为一个完全平方式,则 的值是( )A、
5. 要使 成为一个完全平方式,则 的值是( )A、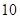 B、
B、 C、20
D、
C、20
D、 6. 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形(如图).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
6. 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形(如图).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )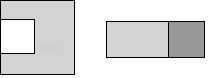 A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣ab=a(a﹣b)7. 已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘为x2﹣4,乙与丙相乘为x2+15x﹣34,则甲与丙相加的结果与下列哪一个式子相同?( )A、2x+19 B、2x﹣19 C、2x+15 D、2x﹣158. 将多项式4x2+1再加上一项,使它能分解因式成(a+b)2的形式,以下是四位学生所加的项,其中错误的是( )A、2x B、﹣4x C、4x4 D、4x9. 若S=(1﹣ )(1﹣ )(1﹣ )…(1﹣ ),则S的值为( )A、 B、 C、 D、10. 设x,y为实数,5x2+4y2﹣8xy+2x+4的最小值为( )A、1 B、2 C、3 D、5
A、a2﹣b2=(a+b)(a﹣b) B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、a2﹣ab=a(a﹣b)7. 已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘为x2﹣4,乙与丙相乘为x2+15x﹣34,则甲与丙相加的结果与下列哪一个式子相同?( )A、2x+19 B、2x﹣19 C、2x+15 D、2x﹣158. 将多项式4x2+1再加上一项,使它能分解因式成(a+b)2的形式,以下是四位学生所加的项,其中错误的是( )A、2x B、﹣4x C、4x4 D、4x9. 若S=(1﹣ )(1﹣ )(1﹣ )…(1﹣ ),则S的值为( )A、 B、 C、 D、10. 设x,y为实数,5x2+4y2﹣8xy+2x+4的最小值为( )A、1 B、2 C、3 D、5二、填空题
-
11. 计算(x-3y ) ( x +3y)的结果是12. 计算:20182-2017×2019= .13. 多项式 加上一个单项式后,使它能成为一个整式的完全平方,那么加上的单项式可以是 . (填上一个你认为正确的即可)
14. 已知x,y满足方程组 ,则x2-4y2的值为。15. 已知(a﹣2017)2+(2018﹣a)2=5,则(a﹣2017)(a﹣2018)=16. 当x= -1时,代数式x2+2x+2的值是 .三、解答题
-
17. 已知:x2﹣y2=12,x+y=3,求2x2﹣2xy的值.18. 已知(m﹣n)2=8,(m+n)2=2,求m2+n2的值.19. 应用乘法公式进行简便运算:(1)、1232﹣122×124;(2)、(﹣79.8)2 .20. 用乘法公式计算下列各式的值
(1)、(2)、(2+1)(22+1)(24+1)⋯(22n+1)21. 小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是am,下底都是bm,高都是(b-a)m. (1)、求小红家这块L形菜地的面积.(用含a、b的代数式表示)(2)、若a2+b2=15,ab=5,求小红家这块L形菜地的面积.
(1)、求小红家这块L形菜地的面积.(用含a、b的代数式表示)(2)、若a2+b2=15,ab=5,求小红家这块L形菜地的面积.
22. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案: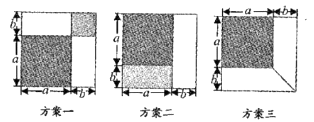
小明发现这三种方案都能验证公式:
a2+2ab+b2=(a+b)2 ,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二,方案三,写出公式的验证过程。
23. 阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如 .善于思考的小明进行了以下探索:
设 (其中a、b、m、n均为整数),则有 .
∴ .这样小明就找到了一种把类似 的式子化为平方式的方法。
请你仿照小明的方法探索并解决下列问题:(a,b,m,n均为正整数)
(1)、 ,用含m、n的式子分别表示a、b,得:a= , b=;
(2)、当a=7,n=1时,填空:7+ =(+ )2
(3)、若 ,求a的值.