2018-2019学年初中数学浙教版七年级下册3.3多项式的乘法同步练习

试卷更新日期：2019-02-27 类型：同步测试

进入出卷网下载

一、单选题

1. 计算（a﹣2）（a+3）的结果是（）

A、a²﹣6 B、a²+a﹣6 C、a²+6 D、a²﹣a+6

查看试题解析
2. 选若(x+3)(x-5)=x²+mx-15，则m等于（）

A、-2 B、2 C、-5 D、5

查看试题解析
3. 若（x﹣2）（x+3）=x²+ax+b，则a、b的值分别为（）

A、a=5，b=6 B、a=1，b=﹣6 C、a=1，b=6 D、a=5，b=﹣6

查看试题解析
4. 若（x+a）（x+2）的计算结果中不含x的一次项，则a的值是（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、2 D、-2

查看试题解析
5. 若多项式x⁴+mx³+nx﹣16含有因式（x﹣2）和（x﹣1），则mn的值是（）

A、100 B、0 C、﹣100 D、50

查看试题解析
6. 若一个长方体的长、宽、高分别是3x－4，2x－1和x，则它的体积是（）

A、6x³－5x²＋4x B、6x³－11x²＋4x C、6x³－4x² D、6x³－4x²＋x＋4

查看试题解析
7. 三个连续的奇数，若中间一个为a，则它们的积为（）

A、a³﹣4a B、a³﹣6a C、4a³﹣a D、4a³﹣6a

查看试题解析
8. (3a+2)(4a²－a－1)的结果中二次项系数是（）

A、－3 B、8 C、5 D、－5

查看试题解析
9. 已知多项式ax+b与2x²﹣x+2的乘积展开式中不含x的一次项，且常数项为﹣4，则a^b的值为（）

A、﹣2 B、2 C、﹣1 D、1

查看试题解析
10. 由 $m (a + b + c) = ma + mb + mc$ ，可得：
$(a + b) (a^{2} - ab + b^{2}) = a^{3} - a^{2} b + {ab}^{2} + a^{2} b - {ab}^{2} + b^{3} = a^{3} + b^{3}$ ，
即 $(a + b) (a^{2} - ab + b^{2}) = a^{3} + b^{3}$ ．①
我们把等式①叫做多项式乘法的立方公式．
下列应用这个立方公式进行的变形不正确的是（）

A、 $(x + 4 y) (x^{2} - 4 xy + 16 y^{2}) = x^{3} + 64 y^{3}$ B、 $(2 x + y) (4 x^{2} - 2 xy + y^{2}) = 8 x^{3} + y^{3}$ C、 $x^{3} + 27 = (x + 3) (x^{2} - 3 x + 9)$ D、 $(a + 1) (a^{2} + a + 1) = a^{3} + 1$

查看试题解析

二、填空题

11. 已知m+n=mn，则（m﹣1）（n﹣1）= ．

查看试题解析
12. 一个三角形的底边长为（2a+6b），高是（3a﹣5b），则这个三角形的面积是．

查看试题解析
13. 已知：x=2a-b-c，y=2b-c-a，z=2c-a-b，则：（b-c）x+（c-a）y+（a-b）z的值是。

查看试题解析
14. 若a²+a+2 013＝2 014，则(5-a)(6+a)＝

查看试题解析
15. 已知a、b都是不为零的常数，如果多项式(x+a)(x+b)的乘积中不含x项，则a+b=

查看试题解析
16. 已知 ${(2 x - 1)}^{5} = a_{5} x^{5} + a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ 是关于 $x$ 的恒等式，则 $a_{0} =$ ．且 $a_{5} - a_{4} + a_{3} - a_{2} + a_{1} =$ ．

查看试题解析

三、解答题

17. 已知长方形的长是（a+3b）米，宽是（a+2b）米．求它的周长和面积．

查看试题解析
18. 已知a₁ ， a₂ ， a₃ ， …，a₂₀₁₅都是正整数，设：M=（a₁+a₂+a₃+…+a₂₀₁₄）（a₂+a₃+…+a₂₀₁₅），N=（a₁+a₂+a₃+…+a₂₀₁₅）（a₂+a₃+…+a₂₀₁₄），试着比较M，N的大小．

查看试题解析
19. 如图，学校的课外生物小组的实验园地是一块长35米，宽26米的长方形，为了行走方便和便于管理，现要在中间修建同样宽的道路，路宽均为a米，余下的作为种植面积，求种植面积是多少？

查看试题解析
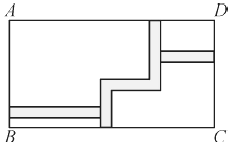20. 已知m²﹣m﹣2=0，求代数式m（m﹣1）+（m+1）（m﹣2）的值．

查看试题解析
21. 一些代数恒等式可以用平面几何图形的面积来表示，例如：(2a＋b)(a＋b)＝2a2＋3ab＋b2就可以用图1或图2等图形的面积来表示．

(1)、请写出下图所表示的代数恒等式：；

(2)、试画出一个几何图形，使它的面积能表示为：(a＋b)(a＋3b)＝a²＋4ab＋3b²；

(3)、请仿照上述方法另写一个含有a、b的代数恒等式，并画出与之对应的几何图形．

查看试题解析
22.

(1)、若关于 $x$ 的多项式 $(x^{2} + x - n) (m x - 3)$ 的展开式中不含 $x^{2}$ 和常数项，求 $m, n$ 的值。

(2)、若n为正整数，且 $x^{2 n} = 4$ ，求 ${(3 x^{3 n})}^{2} - 4 {(- x^{2})}^{2 n}$ 的值。

查看试题解析
23. 先化简，再求值：2(a＋ $\sqrt{3}$ )(a－ $\sqrt{3}$ )－a(a－6)＋6，其中a＝ $\sqrt{2}$ －1.

查看试题解析
24. 计算：

(1)、（5mn²﹣4m²n）（﹣2mn）

(2)、（x+7）（x﹣6）﹣（x﹣2）（x+1）

查看试题解析

2018-2019学年初中数学浙教版七年级下册3.3多项式的乘法 同步练习

一、单选题

二、填空题

三、解答题

2018-2019学年初中数学浙教版七年级下册3.3多项式的乘法同步练习