辽宁省辽阳市2018-2019学年高二上学期理数期末考试试卷
试卷更新日期:2019-02-25 类型:期末考试
一、单选题
-
1. 设命题: , ,则 为( )A、
 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  2. 在等差数列 中,若 , 是方程 的两个根,则 ( )A、
2. 在等差数列 中,若 , 是方程 的两个根,则 ( )A、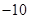 B、
B、 C、
D、
3. 椭圆 的离心率为( )A、 B、 C、 D、
C、
D、
3. 椭圆 的离心率为( )A、 B、 C、 D、 4. 不等式 的解集为( )A、
4. 不等式 的解集为( )A、 B、
B、 或
或  C、
C、 D、
D、 或
或  5. 已知双曲线 的离心率 ,且其虚轴长为8,则双曲线 的方程为( )A、
5. 已知双曲线 的离心率 ,且其虚轴长为8,则双曲线 的方程为( )A、 B、
B、 C、
C、 D、
D、 6. 在三棱柱 中,若 , , ,则A、
6. 在三棱柱 中,若 , , ,则A、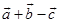 B、
B、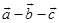 C、
C、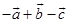 D、
D、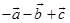 7. 若等比数列 的前 项和为 , ,则 ( )A、 B、1 C、
7. 若等比数列 的前 项和为 , ,则 ( )A、 B、1 C、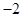 D、
D、 8. 设直线 的方向向量为 ,平面 的法向量为 , ,则使 成立的是( )A、
8. 设直线 的方向向量为 ,平面 的法向量为 , ,则使 成立的是( )A、 ,
,  B、
B、 ,
, 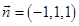 C、
C、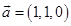 ,
,  D、
D、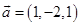 ,
, 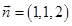 9. “方程 表示的曲线为椭圆”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件10. 已知空间向量 ,平面 的一个法向量为 ,则直线 与平面 所成角 为( )A、 B、
9. “方程 表示的曲线为椭圆”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件10. 已知空间向量 ,平面 的一个法向量为 ,则直线 与平面 所成角 为( )A、 B、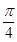 C、
C、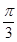 D、
D、 11. 已知 , ,且 .若 恒成立,则 的取值范围为( )A、
11. 已知 , ,且 .若 恒成立,则 的取值范围为( )A、 B、
B、 C、
C、 D、
D、 12. 设双曲线 ( , )的上顶点为 ,直线 与 交于 , 两点,过 , 分别作 , 的垂线交于点 ,若 到点 的距离不超过 ,则 的离心率的取值范围是( )A、
12. 设双曲线 ( , )的上顶点为 ,直线 与 交于 , 两点,过 , 分别作 , 的垂线交于点 ,若 到点 的距离不超过 ,则 的离心率的取值范围是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 若 满足约束条件 ,则 的最小值为 .14. 命题“当 时,若 ,则 .”的逆命题是 .15. 已知 是抛物线 的焦点, , 是该抛物线上的两点, ,则线段 的中点到 轴的距离为 .16. 如图,在三棱锥 , 为等边三角形, 为等腰直角三角形, ,平面 平面 , 为 的中点,则异面直线 与 所成角的余弦值为 .

三、解答题
-
17. 设 是公比为正数的等比数列,若 ,且 , ,8成等差数列.(1)、求 的通项公式;(2)、设 ,求证:数列 的前n项和 .18. 已知 ,且 ,设 函数 在 上单调递增; 函数 在 上的最小值大于 .(1)、试问 是 的什么条件?为什么?(2)、若命题 为假,命题 为真,求 的取值范围.19. 已知过 的直线 与抛物线 交于点 , .(1)、若 为弦 的中点,求直线 的方程;(2)、若 为抛物线 的焦点, 为抛物线 上的动点,求 的最小值.20. 如图,菱形 的边长为4, ,矩形 的面积为 ,且平面 平面 .
 (1)、证明: ;(2)、求二面角 的正弦值.
(1)、证明: ;(2)、求二面角 的正弦值.