河北省省级示范高中联合体2018-2019学年高三上学期文数12月联考试卷
试卷更新日期:2019-02-25 类型:高考模拟
一、单选题
-
1. 若 ,则 ( )A、 B、 C、
 D、
D、 2. 设集合 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 某学校的老师配置及比例如图所示,为了调查各类老师的薪资状况,现采用分层抽样的方法抽取部分老师进行调查,在抽取的样本中,青年老师有30人,则该样本中的老年教师人数为( )
2. 设集合 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 某学校的老师配置及比例如图所示,为了调查各类老师的薪资状况,现采用分层抽样的方法抽取部分老师进行调查,在抽取的样本中,青年老师有30人,则该样本中的老年教师人数为( ) A、 B、 C、18 D、204. 曲线 在点 处的切线的斜率为( )A、
A、 B、 C、18 D、204. 曲线 在点 处的切线的斜率为( )A、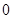 B、1
C、
B、1
C、 D、
D、 5. 已知 ,且 ,则 ( )A、
5. 已知 ,且 ,则 ( )A、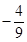 B、
B、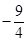 C、
D、
6. 某三棱锥的三视图如图所示,则该棱锥最长的棱长为( )
C、
D、
6. 某三棱锥的三视图如图所示,则该棱锥最长的棱长为( ) A、 B、 C、 D、
A、 B、 C、 D、 7. 的内角 , , 的对边分别为 , , .若 , , ,则 ( )A、
7. 的内角 , , 的对边分别为 , , .若 , , ,则 ( )A、 B、
B、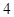 C、
C、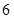 D、
D、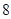 8. 设 , 满足约束条件 ,则 的取值范围为( )A、
8. 设 , 满足约束条件 ,则 的取值范围为( )A、 B、
B、 C、
C、 D、
D、 9. 若函数 在 上单调递增,则 的取值范围是( )A、
9. 若函数 在 上单调递增,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 10. 袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
10. 袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到“和”“平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:232 321 230 023 123 021 132 220 011 203 331 100
231 130 133 231 031 320 122 103 233 221 020 132
由此可以估计,恰好第三次就停止的概率为( )
A、 B、
C、
D、
B、
C、
D、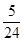 11. 设 , ,则 ( )A、
11. 设 , ,则 ( )A、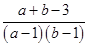 B、
B、 C、
C、 D、
D、 12. 已知椭圆 的右焦点为 , 为 上的动点, ,若 的周长的最大值为 ,则 的离心率为( )A、
12. 已知椭圆 的右焦点为 , 为 上的动点, ,若 的周长的最大值为 ,则 的离心率为( )A、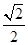 B、
C、
D、
B、
C、
D、
二、填空题
-
13. 已知向量 , 的夹角为 ,且 ,则 .14. 函数 在 上的值域为 .15. 已知直线 经过双曲线 的右顶点,且 与 的两条渐线分别交于 , 两点,则 .16. 设圆锥的顶点与底面圆周都在球 的表面上,且该圆锥的母线与底面所成角为 ,圆锥的底面半径为1,则球 的表面积为 .
三、解答题
-
17. 设 为等差数列 的前 项和, , .(1)、求 的通项公式;(2)、若 成等比数列,求 .18. 某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值
频数
6
26
38
22
8
质量指标值分组
频数
频率
6
0.06
合计
100
1
 (1)、将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;(2)、估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).19. 如图,在三棱锥 中, 平面 , , , .
(1)、将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;(2)、估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).19. 如图,在三棱锥 中, 平面 , , , . (1)、证明:平面 平面 ;(2)、设棱 , 的中点分别 , ,点 为棱 上一点,若 为等腰直角三角形,求三棱锥 的体积.20. 在直角坐标系 中,直线 与抛物线 交于 , 两点,且 .(1)、求 的方程;(2)、试问:在 轴的正半轴上是否存在一点 ,使得 的外心在 上?若存在,求 的坐标;若不存在,请说明理由..
(1)、证明:平面 平面 ;(2)、设棱 , 的中点分别 , ,点 为棱 上一点,若 为等腰直角三角形,求三棱锥 的体积.20. 在直角坐标系 中,直线 与抛物线 交于 , 两点,且 .(1)、求 的方程;(2)、试问:在 轴的正半轴上是否存在一点 ,使得 的外心在 上?若存在,求 的坐标;若不存在,请说明理由..