四川省雅安市2017-2018学年高一上学期数学期末考试试卷
试卷更新日期:2019-02-25 类型:期末考试
一、单选题
-
1. 已知集合 ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 若函数 是幂函数,则 的值为( )A、 B、0 C、1 D、23. 已知函数 ,则 ( )A、4 B、1 C、0 D、4. 若 ,则 =( )A、5 B、6 C、7 D、5. 已知 ,则 值为( )A、 B、 C、
2. 若函数 是幂函数,则 的值为( )A、 B、0 C、1 D、23. 已知函数 ,则 ( )A、4 B、1 C、0 D、4. 若 ,则 =( )A、5 B、6 C、7 D、5. 已知 ,则 值为( )A、 B、 C、 D、
D、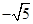 6. 已知函数 在 上为增函数,则实数 的取值范围是( )A、
6. 已知函数 在 上为增函数,则实数 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 7. 已知 ,若 ,则 ( )A、
7. 已知 ,若 ,则 ( )A、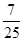 B、
B、 C、
C、 D、1
8. 函数 的零点是 和 ,则 ( )A、 B、 C、 D、
D、1
8. 函数 的零点是 和 ,则 ( )A、 B、 C、 D、 9. 已知全集为 ,函数 的定义域为集合 ,且 ,则 的取值范围是( )A、
9. 已知全集为 ,函数 的定义域为集合 ,且 ,则 的取值范围是( )A、 B、
B、 C、 或
C、 或  D、
D、 或
或  10. 函数 的局部图象如图所示,为了得到 的图象,只需将 的图象( )
10. 函数 的局部图象如图所示,为了得到 的图象,只需将 的图象( ) A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位11. 已知定义在 上的函数 在 上是减函数,若 是奇函数,且 ,则不等式 的解集是( )A、
A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位11. 已知定义在 上的函数 在 上是减函数,若 是奇函数,且 ,则不等式 的解集是( )A、 B、
B、 C、
C、 D、
D、 12. 设函数 是定义在 上的偶函数,对任意 ,都有 ,且当 时, ,若在区间 内关于 的方程 至少有2个不同的实数根,至多有3个不同的实数根,则 的取值范围是( )A、
12. 设函数 是定义在 上的偶函数,对任意 ,都有 ,且当 时, ,若在区间 内关于 的方程 至少有2个不同的实数根,至多有3个不同的实数根,则 的取值范围是( )A、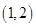 B、
B、 C、
C、 D、
D、
二、填空题
-
13. .14. 函数 的图象恒过定点 ,点 在指数函数 的图象上,则 .15. 在 中, , 边上的高等于 ,则 .16. 设 是定义在 上的增函数,且 ,若 ,则当 时, 的取值范围是 .
三、解答题
-
17.(1)、计算: ;(2)、已知 都是锐角, ,求 的值.18. 设函数 .(1)、求函数 图象的对称轴;(2)、求函数 的单调递增区间.19. 已知函数 且 , .(1)、求函数 的定义域;(2)、当 时,判断函数 在定义域内的单调性,并用函数单调性定义证明.
