河北省邢台市2018-2019学年高三上学期文数一轮摸底考试(12月)试卷
试卷更新日期:2019-02-25 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、
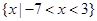 B、
B、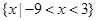 C、
C、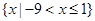 D、
D、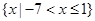 2. 设 的实部与虚部相等,其中 为实数,则 ( )A、-1 B、-2 C、1 D、23. 某几何体的三视图如图所示,则该几何体的直观图为( )
2. 设 的实部与虚部相等,其中 为实数,则 ( )A、-1 B、-2 C、1 D、23. 某几何体的三视图如图所示,则该几何体的直观图为( )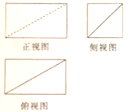 A、
A、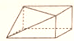 B、
B、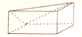 C、
C、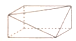 D、
D、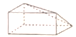 4. ( )A、
4. ( )A、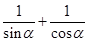 B、
B、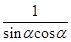 C、
C、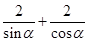 D、
D、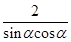 5. 若双曲线 的离心率为2,则其实轴长为( )A、 B、 C、 D、
5. 若双曲线 的离心率为2,则其实轴长为( )A、 B、 C、 D、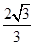 6. 函数 的图像大致为( )A、
6. 函数 的图像大致为( )A、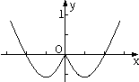 B、
B、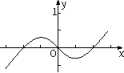 C、
C、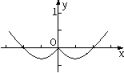 D、
D、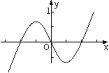 7. 若 , 满足约束条件 则 的最小值为( )A、
7. 若 , 满足约束条件 则 的最小值为( )A、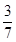 B、
C、0
D、
B、
C、0
D、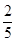 8. 下列函数满足 的是( )A、
8. 下列函数满足 的是( )A、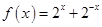 B、
B、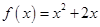 C、
C、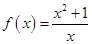 D、
D、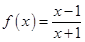 9. 函数 在 上的最小值为( )A、
9. 函数 在 上的最小值为( )A、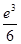 B、
B、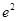 C、
C、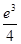 D、
D、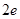 10. 的内角 , , 的对边分别为 , , .已知 , , 成等比数列, ,且 ,则 ( )A、
10. 的内角 , , 的对边分别为 , , .已知 , , 成等比数列, ,且 ,则 ( )A、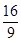 B、
C、
B、
C、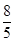 D、
11. 已知三棱锥 的侧棱两两垂直, , , 为棱 上的动点, 与侧面 所成角为 ,则 的最大值为( )A、
D、
11. 已知三棱锥 的侧棱两两垂直, , , 为棱 上的动点, 与侧面 所成角为 ,则 的最大值为( )A、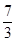 B、
B、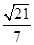 C、
C、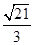 D、
D、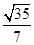 12. 将函数 的图像向左平移 个单位长度后,得到 的图像,若函数 在 上单调递减,则正数 的最大值为( )A、 B、1 C、 D、
12. 将函数 的图像向左平移 个单位长度后,得到 的图像,若函数 在 上单调递减,则正数 的最大值为( )A、 B、1 C、 D、二、填空题
-
13. 已知向量 , 满足 , , ,则 .14. 若一个底面半径为1,高为2的圆柱的两个底面的圆周都在球 的表面上,则球 的表面积为 .15. 小周公司的班车早上7点到达 地,停留15分钟.小周在6:50至7:45之间到达 地搭乘班车,且到达 地的时刻是随机的,则他能赶上公司班车的概率为 .16. 点 在椭圆 上, 的右焦点为 ,点 在圆 上,则 的最小值为 .
三、解答题
-
17. 在数列 中, ,且 , , 成等比数列.(1)、求 , , ;(2)、求数列 的前 项和 .18. 甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
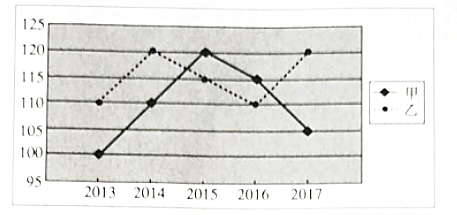
(附: , )
(1)、根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;(2)、根据乙这五年年度体检血压值的数据,求年度体检血压值 关于年份 的线性回归方程,并据此估计乙在2018年年度体检的血压值.19. 如图,在三棱锥 中, 平面 ,且 , .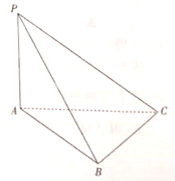 (1)、证明: 为直角三角形;(2)、设 在平面 内的射影为 ,求四面体 的体积.20. 在直角坐标系 中,曲线 与直线 交于 , 两点.(1)、当 时,求 的面积的取值范围;(2)、 轴上是否在点 ,使得当 变动时,总有 ?若存在,求以线段 为直径的圆的方程;若不存在,请说明理由.
(1)、证明: 为直角三角形;(2)、设 在平面 内的射影为 ,求四面体 的体积.20. 在直角坐标系 中,曲线 与直线 交于 , 两点.(1)、当 时,求 的面积的取值范围;(2)、 轴上是否在点 ,使得当 变动时,总有 ?若存在,求以线段 为直径的圆的方程;若不存在,请说明理由.